Chciałbyś dowiedzieć się więcej? Koniecznie przeczytaj artykuł: Akcja aktywacja, czyli za pomocą jakich metod aktywizować uczniów na lekcji matematyki?
POLECAMY
Przedstawię Państwu różne gry i zabawy, które sprawią, że uczniowie chętniej będą się uczyć – czasami nie mając świadomości, że to, co robią, to nie jest tylko zabawa. Moje propozycje są do wykorzystania w pracy zarówno z dziećmi, jak i z młodzieżą oraz dorosłymi.
Zacznijmy od tego, że nasz mózg nie lubi nudy. Ciągle musi coś robić. Jeśli my nie damy mu zajęcia, zajmie się czymś mało ważnym – z naszego punktu widzenia. Nie raz możemy spotkać się z sytuacją, gdy uczeń podczas lekcji buja w obłokach. Jest to sygnał dla nauczyciela, że to, co się dzieje w klasie, dla mózgu tego konkretnego ucznia jest mało atrakcyjne. W związku z tym znalazł sobie bardziej interesujące zajęcie, na przykład liczenie liści na drzewie za oknem. No cóż, nie uda się nam zadowolić wszystkich, ale możemy się starać, aby pozytywnie zaangażować jak największą grupę uczniów. Zwiększamy swoje szanse, jeśli pozwolimy im korzystać z własnej wyobraźni. Co zatem możemy zaproponować, aby lekcje stały się ciekawsze (przynajmniej z punktu widzenia mózgu)?
Jedną z technik, którą możemy wykorzystać na matematyce, są haki pamięciowe. Istnieje wiele odmian tej metody, ja przedstawię dwie najbardziej popularne.
Obrazkowe haki pamięciowe
Metoda polega na tym, by dla każdej cyfry od zera do dziewięciu dobrać obraz, który będzie ją reprezentował. Skojarzeń może być bardzo dużo, ja pokażę te, które sama stosuję i lubię. Nie przeszkadza to, aby każdy z Was i Waszych uczniów stworzył własny system. Moje haki wyglądają tak jak na rycinie 1.

Przypisałam następujące obrazy do kolejnych cyfr:
0 – balon
1 – świeca
2 – łabędź
3 – serce
4 – krzesło
5 – hak
6 – słoń
7 – kosa (jestem z pokolenia, które zna ten przedmiot, ale można wybrać na przykład chorągiewkę)
8 – bałwan
9 – rakieta tenisowa
Kiedy obrazy i cyfry są dla nas jednoznaczne, możemy przystąpić do kodowania różnych informacji. Na przykład zapamiętania kwadratów liczb większych od 10.
11 razy 11 to 121. Zatem muszę wyobrazić sobie świecę (1), łabędzia (2) i kolejną świecę (1). Obrazy muszą pojawić się w tej właśnie kolejności, aby zachować porządek cyfr w liczbie. Muszę stworzyć teraz historię, którą zapamiętam, bo będzie absurdalna, głupia, śmieszna albo dziwna. Zaangażuje moją wyobraźnię i emocje. Na przykład taką: trzymając wielką świecę, idę przez ciemność, nic nie widzę, jest mi zimno i zaczynam się bać. Nagle z naprzeciwka coś do mnie się zbliża. Czuję mrowienie na plecach. Zatrzymuję się i czekam. W tym momencie orientuję się, że zbliża się do mnie łabędź, też jest zagubiony i przestraszony. Ma nawet świecę, tyle że jego świeca jest zgaszona. Przyglądam się tej zgaszonej świecy i widzę czerwoną kwadratową nalepkę z liczbą 11 (lub opcjonalnie z dwoma świecami). Taka historia pozwala na zapamiętanie informacji, że 11 do kwadratu to 121. Spróbujcie z uczniami wymyśleć historie dotyczące kolejnych liczb podniesionych do kwadratu.
A co, jeżeli mamy do zapamiętania inne potęgi liczby? Tu też z pomocą przychodzi wyobraźnia. Trzecia potęga to sześcian, czyli wystarczy do naszego obrazu dołączyć znany i charakterystyczny sześcienny przedmiot. Może to być kostka do gry, pudełko czy układanka. Jeśli kwadrat i sześcian to za mało, musimy wprowadzić nowy obraz, który zawsze będzie nam się kojarzył z potęgą. W moim przypadku jest to korona. Symbol władz i siły, czyli potęgi. Umieszczając koronę w moim obrazie, daję mózgowi sygnał, że mam do czynienia z potęgą.
Jeśli chcemy tę technikę wykorzystywać częściej na lekcji matematyki, warto stworzyć swoje obrazy dla działań matematycznych oraz najpopularniejszych symboli. Ćwiczenie czyni mistrza, więc trenujcie wyobraźnię swoją i swoich uczniów.
Rymowane haki pamięciowe
Technika jest podobna do poprzedniej – z tą różnicą, że haki wybieramy nie na zasadzie podobieństwa kształtu, ale rymu. I tak na przykład ja mam następujące zakładki:
0 – ksero
1 – Eden
2 – drwa
3 – wszy
4 – rowery
5 – pięść
6 – teść
7 – tandem
8 – prosię
9 – pieczęć
Wy, oczywiście, możecie wybrać inne. Zasada jest jednak taka, aby znaleźć rym i aby nowe słowo było łatwe do wyobrażenia. Jeśli rym będzie zbyt skomplikowany, może to utrudnić stosowanie metody.
Powyższe propozycje nie są jedyne. System haków może być bardzo dowolny. Ważne, aby był nam dobrze znany i stały. Istnieją zakładki osobiste związane z częściami ciała. Zakładki mieszkaniowe (rzymski pokój), gdy wybieramy charakterystyczne punkty naszego mieszkania lub pokoju. Ponieważ metody haków bazują na łączeniu nowych informacji ze starymi, hakami mogą być dowolne znane nam listy, na przykład planety ustawione w kolejności od słońca. Jednak takie zakładki sprawdzą się, jeśli mamy wiadomości na temat poszczególnych planet. W przeciwnym razie możemy nie rozróżnić kolejnych haków i wprowadzimy zamieszanie. Jeśli Ty lub Twój uczeń jesteście pasjonatami jakiejś dziedziny, możecie wybrać zakładki związane ze swoją pasją.
Rysowanki i rebusy
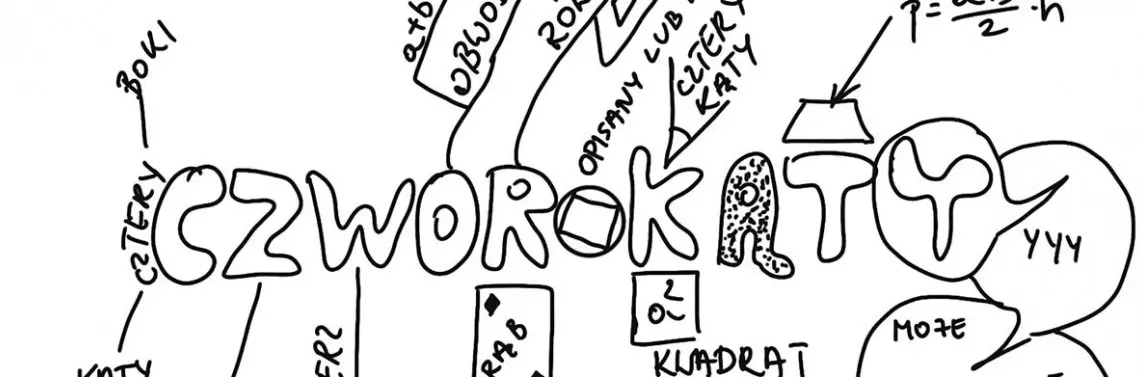
Kiedy mamy zebrać i powtórzyć wiadomości z jakiegoś działu czy tematu, ciekawą zabawą jest narysowanie słowa, które reprezentuje nasz temat. Następnie do każdej litery wybranego wyrazu dopisujemy wiadomości i informacje w taki sposób, aby zaczynały się one na wskazaną literę. Tworzenie takiego obrazka powoduje, że przede wszystkim musimy określić, czego dotyczy cały dział, a potem zapisać to za pomocą słowa lub dwóch. Następnie zbieramy informacje i musimy przełożyć je na zrozumiały język – z zachowaniem zasady, że informacja musi rozpoczynać się na konkretną literę. Efekt takiej pracy mógłby wyglądać tak jak na rycinie 2.

Tworzenie rebusów również jest fajną zabawą, pozwalającą na utrwalenie matematycznego nazewnictwa. Trzeba tylko pamiętać, że nie wszystko to, co dla nas jest oczywiste, dzieci odczytają w ten sam sposób. Tak jest na przykład z hasłem: siatka graniastosłupa. Jako rebus narysowałabym to tak, jak na rycinie 3.
Problem może polegać na tym, że coś, co ja pamiętam pod nazwą siatki, moje dzieci nazywają na przykład reklamówką lub torbą na zakupy.

Takie rysowanie rebusów sprawdzi się na pewno w szkole podstawowej, natomiast w szkole średniej można poprosić uczniów o wykonanie pracy w domu. Może w ten sposób powstać matematyczna gazetka dla osób lubiących rozwiązywać zagadki.
Zbieranie i powtarzanie informacji w inny sposób niż zwykle
Kolejną propozycją na powtórzenie informacji przed klasówką czy egzaminem jest metoda ABC. Polega ona na tym, że wypisujemy wszystkie litery alfabetu, od A do Z, pomijając te z polskimi znakami diakrytycznymi. Jeśli na późniejszym etapie okaże się, że możemy je wykorzystać, po prostu je dopiszemy. Teraz, kiedy mamy już listę liter, do każdej z nich dopisujemy informację dotyczącą tematu, który powtarzamy. Zasada dopisywania jest taka, że informacja, którą dopisujemy, zaczyna się na wskazaną literę (dlatego sugerowałam pominięcie liter ą, ę itp.). Naszym celem jest zapisanie wszystkiego, co wiemy na dany temat, oraz znalezienie pary dla każdej litery. Oczywiście, może się zdarzyć, że nie jesteśmy w stanie dopasować hasła rozpoczynającego się na przykład literą C. Mamy wówczas trzy możliwości. Po pierwsze – zostawiamy literę bez dopasowania. Po drugie – próbujemy przeredagować inne hasła, może jednak się uda. Po trzecie – zdajemy się na naszą i uczniów kreatywność. Możemy zacząć wpis na przykład tak: coś mi się wydaje, że… Niektóre litery dopasowuje się łatwiej, inne trudniej. Nie należy się zniechęcać, gdy mamy kilka haseł na jedną literę. Zapiszmy je, być może później przyjdzie nam do głowy inne skojarzenie i będziemy mogli przepisać je w puste miejsce.
Taką zabawę można wykorzystać w pracy indywidualnej lub na lekcji z klasą. Możemy również łączyć obie formy. Wyobraźmy sobie, że zbieramy wiadomości dotyczące własności funkcji. Możemy poprosić uczniów, aby każdy – sam lub z kolegą z ławki – wypisał własne skojarzenia. Następnie tworzymy na tablicy wspólną listę ABC. Prosimy uczniów, aby uzupełnili ją swoimi propozycjami. Niektóre skojarzenia się powtórzą (wówczas zapisujemy je tylko raz), inne będą unikatowe. W ten sposób powstanie ciekawa baza wiedzy, która może wyglądać na przykład tak:
A – a to litera, która często występuje we wzorze ogólnym funkcji, mogą być również inne litery
B – bez wykorzystania wszystkich argumentów nie ma mowy o funkcji
C – ciągła funkcja w punkcie lub przedziale
D – dziedzina, czyli zbiór argumentów; działania na funkcjach
E – ewentualnie przydaje się znajomość granic i pochodnych funkcji
F – f (x) taki symbol oznacza funkcję f o argumencie x
G – graf
H – Homogeniczna funkcja, co to właściwie jest? Czy muszę to znać?
I – i nie zapomnij, że każdemu argumentowi przyporządkowana jest dokładnie jedna wartość
J – Jak mogę wykorzystać znajomość funkcji? Może przyda mi się przy obliczaniu najbardziej optymalnego rozwiązania
K – kwantyfikatory stosujemy, gdy mamy zapisać symbolem, że coś jest prawdziwe dla wszystkich lub tylko dla niektórych x
L – linia może być wykresem funkcji, ale czasami wykresem są punkty
Ł – łatwo się pogubić, jeśli nie określimy poprawnie dziedziny i przeciwdziedziny
M – miejsca zerowe funkcji; monotoniczność
N – nierosnąca i niemalejąca funkcja
O – odwzorowanie zbioru X w/na zbiór Y; odwrotna funkcja; okres funkcji
P – przeciwdziedzina, czyli zbiór wartości; parzystość funkcji
R – równość funkcji; różnowartościowość
S – stała funkcja
T – tabelka argumentów i wartości funkcji
U – układ współrzędnych, w nim rysujemy wykres funkcji
W – wzór funkcji; wykres funkcji
X – x tak zwykle oznaczamy argument funkcji
Y – y tak zwykle oznaczamy wartość funkcji
Z – złożenie funkcji
I tak jak poprzednio – nie jest to jedyna możliwa lista ABC dotycząca własności funkcji. Wszystko będzie zależało od tego, z jaką klasą ją tworzymy. Inne treści pojawią się w klasach realizujących program w zakresie podstawowym, a inne, gdy klasa realizuje program rozszerzony. Bez względu na zakres materiału uczeń musi powtórzyć wiadomości, usystematyzować je i zapisać na liście. Oprócz opisów słownych możemy dodać również zapis symbolami lub warunki, które musi spełniać funkcja, abyśmy mogli powiedzieć, że ma konkretną własność.
Jeśli nie chcemy poświęcać czasu na lekcji na tworzenie listy ABC, zawsze warto pokazać uczniom tę metodę, aby mogli wykorzystać ją w domu. Być może w ten sposób będą powtarzali materiał również z innych przedmiotów. Ponadto taka lista może być ciekawą formą ściągi.
Escape room
Ta metoda wymaga od nauczyciela najwięcej przygotowań i pracy. Zasada jest jedna – rozwiązując szereg zadań i problemów, uczniowie mają dojść do wyznaczonego punktu, czyli wyjścia z pokoju zagadek. Pod względem technicznym nauczyciel może skorzystać z wielu rozwiązań. Na przykład z platform internetowych, pozwalających na stworzenie atrakcyjnej formy (np. Genially) i złudzenia, że naprawdę chodzimy po pokoju, szukając wyjścia. Prostszym rozwiązaniem jest skorzystanie z interaktywnych formularzy (np. Google Forms). Możemy też ograniczyć się do zadań na kartkach i ewentualnie zastosować kody qr. Bez względu na to, na jaką formę zdecyduje się nauczyciel, najważniejszy jest scenariusz całej gry. Na początku trzeba zaprojektować pokój zagadek na kartce.
- Jaki jest temat przewodni escape roomu?
- Gdzie i jakie informacje uczeń znajdzie?
- W jaki sposób znalezienie jednej informacji pomoże w rozwiązaniu kolejnego zadania?
- Ile będzie zadań?
- Jaki jest czas na rozwiązanie wszystkich zagadek?
- Co w sytuacji, gdy uczniowie napotkają trudności? Czy mają możliwość skorzystania z podpowiedzi? Ile tych podpowiedzi mogą uzyskać i od kogo?
- Jak wygląda planowana trasa przejścia ucznia przez wszystkie zagadki? Czy uczeń może pójść inaczej? Czy nie ułatwi to zadania?
- Dobieramy i testujemy zadania. Chodzi o to, by uczniowie nie natknęli się na trudności, których dla nich nie zaplanowaliśmy.
- Tworzymy escape room w sposób, jaki sobie wybierzemy (platforma internetowa, formularze, kartki).
- Na koniec prosimy kilka osób, aby spróbowały przejść całą grę i powiedziały, co sprawiło największą trudność, a co było za łatwe. Być może nie zauważyliśmy, że można pominąć jakiś etap. Teraz jest czas na uwagi i poprawki.
- Dajemy uczniom gotowy produkt.
Tego typu zabawa jest z reguły lubiana przez uczniów. Musimy mieć jednak świadomość, że jedna godzina takich zajęć może się wiązać z kilkoma godzinami przygotowań. Szczególnie, jeśli tworzymy pokój zagadek po raz pierwszy lub dopiero uczymy się nowego narzędzia. Dobrą praktyką jest wymienianie się nauczycieli gotowymi scenariuszami i adresami internetowymi, pod którymi są gotowe pokoje. Pomocne mogą być również książki. Kilka lat temu pojawiły się cztery książki z serii „Matematyczne śledztwo”. Są to: „Zamek zagadek”, w którym trzeba wykazać się wiedzą z zakresu brył, figur i miar; „Muzeum tajemnic”, gdzie niezbędna jest znajomość liczb i działań na nich; „Jaskinia tropów”, która zmusza czytelnika do korzystania z arytmetyki; oraz „Planeta sekretów”, która wymaga, aby korzystać z danych oraz umieć je odczytywać i interpretować.
Mam nadzieję, że zachęciłam Was do wypróbowania kilku gier i zabaw angażujących mózg i ciekawych dla niego form pracy. Nawet jeśli pracujecie z osobami dorosłymi, takie zabawy mogą okazać się przyjemną odskocznią. Nie ryzykujecie nic poza zaangażowaniem Waszych uczniów.