Drukowanie na drukarkach 3D obiektów geometrycznych – obok radości z efektów wydruku – może przynieść jeszcze więcej splendoru z możliwości dydaktycznych w postaci odkrywania ciekawych własności geometrycznych tych obiektów i przystosowania ich do tworzenia interesujących układanek matematycznych.
Przeznaczeniem takich wymyślnych układanek jest na przykład ułożenie z elementów jednego wielościanu innego o tej samej objętości. Nie tylko niosą one za sobą radość z ich układania, ale spostrzegawczemu matematykowi ułatwiają też wykonanie trudnych obliczeń bez skomplikowanych rachunków.
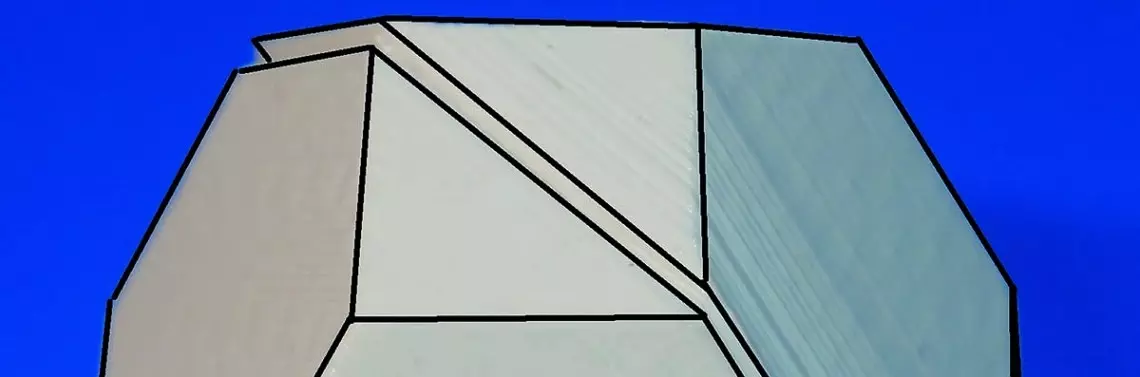
Na ryc. 1 widzimy rozrzucone wielościany. Gdy dokładniej im się przypatrzymy, zauważymy, że są one wszystkie przystające. Jest ich dokładnie osiem. Intuicja podpowiada, że mogą one mieć związek z ośmiościanem foremnym. Ale intuicji nie wolno dowierzać. Czy można z nich coś ułożyć?
POLECAMY

Skoro są jednakowe, to warto je poskładać ze sobą tak, by ich przystające ścianki przylegały do siebie. Zauważmy, że każdy wielościan ma łącznie osiem ścian przystających parami z uwagi na jego symetrię płaszczyznową. W żadnej parze nie powtarzają się przystające ściany.
Odłóżmy cztery z tych wielościanów, a z pozostałych spróbujmy ułożyć jakąś rozsądną figurę, przykładając do siebie przystające ściany. Możemy to uczynić na cztery sposoby, gdyż, jak już wspomnieliśmy, dysponujemy czterema rodzajami ścian. Są to:
- sześciokąt foremny – ryc. 2A,
- sześciokąt różnoboczny – ryc. 2B,
- trójkąt prostokątny duży – ryc. 2C,
- trójkąt prostokątny mały – ryc. 2D.

Sześciokąt foremny sugeruje, że z tych ośmiu elementów możemy złożyć jedną z brył Archimedesa, np. czworościan ścięty, ośmiościan ścięty, sześcioośmiościan ścięty, dwudziestościan ścięty lub dwudziestodwunastościan ścięty.
Złożenie dwóch brył ścianami sześciokątnymi daje konfigurację, w której dwie ściany są prostopadłe (ryc. 3), a dołożenie do nich jeszcze dwóch o takiej samej konfiguracji pozwala nam dostrzec pół sześcianu (ryc. 4).


Kolejne cztery identyczne wielościany formują z już ułożonymi pełen sześcian. Krawędzią tego sześcianu jest najdłuższy bok sześciokąta różnobocznego – ryc. 5.

Inny sposób złożenia otrzymamy dość łatwo – składając ze sobą wielościany ośmiokątami różnobocznymi, najpierw po dwie (ryc. 6), a potem pozostałe dwie. Utworzą one bryłę, która ma dwie prostopadłe płaszczyzny symetrii. Całość prezentuje coś znajomego – ośmiościan ścięty.

Tak więc osiem wielościanów pokazanych na początku artykułu daje albo sześcian, albo dwie przystające bryły Archimedesa – ośmiościany ścięte (ryc. 7A i B).

Ta układanka, w samej naturze prosta, może nam posłużyć do wyznaczenie objętości ośmiościanu ściętego. Odkryliśmy już, że:

Oznaczmy przez „a” długość krawędzi sześcianu, z którego powstały dwa ośmiościany ścięte. Ich krawędzie oznaczmy literą x. Poszukajmy relacji między wielkościami a i x. Znajdziemy je, obserwując ścianę, która jest sześciokątem różnobocznym – figura niebieska na ryc. 8.

Zauważmy, że:

Ponieważ:

więc

To nie jest jedyny sposób wyznaczenia objętości tego wielościanu przez zastąpienie go innymi wielościanami o tej samej objętości. Jeśli wykonamy sześciokątne przekroje dwóch przystających sześcianów, to możemy z nich złożyć połowę ośmiościanu ściętego – ryc. 9 i 10.


Zatem z czterech sześcianów uzyskamy w ten sposób jeden ośmiościan ścięty. Rysunek 11 ilustruje połowę tego ośmiościanu.

Przyjmijmy znowu krawędź każdego z czterech sześcianów jako „a”. Długość „y” krawędzi ośmiościanu ściętego jest długością boku sześciokąta stanowiącego przekrój sześcianu. Bok tego sześciokąta łączy środki dwóch sąsiednich boków kwadratu, który jest ścianą sześcianu – ryc. 12.


Otrzymaliśmy taki sam wynik objętości ośmiościanu ściętego o krawędzi długości „y”.
Na koniec warto wyznaczyć tę objętość metodami klasycznymi. Objętość ośmiościanu ściętego to różnica objętości ośmiościanu foremnego i objętości sześciu ostrosłupów odciętych w jego narożach w 1/3 każdej krawędzi ośmiościanu.
Objętość ośmiościanu foremnego o krawędzi długości „a” jest równa:


I znowu otrzymaliśmy ten sam wynik.
Tak więc mamy przykład zadania geometrycznego rozwiązanego trzema różnymi sposobami. Czytelnik sam oceni, które z tych rozwiązań przedstawia największą wartość dydaktyczną.
Rycina 14 ilustruje początkowe fazy tworzenia układanki zaprojektowanej w darmowym programie SketchUp, która pokazuje, jak dwa ośmiościany ścięte można umieścić w jednym sześcianie.


Autor zna sporo układanek, które z jednych wielościanów przez odpowiednie rozcięcie tworzą inne wielościany. Oczywiście, oba wielościany, mimo iż posiadają tę samą objętość, muszą jeszcze spełniać warunek równoważności przez rozcięcie, czyli III problem Hilbera.
Wiele z nich, precyzyjnie wykonanych na drukarce 3D, można zakupić na stronie www.math-comp-educ.pl. Mają one sporo zalet dydaktycznych, gdyż uczniowie na takich modelach mogą sprawdzać różne własności metryczne tych wielościanów i pogłębiać swoją wyobraźnię przestrzenną.