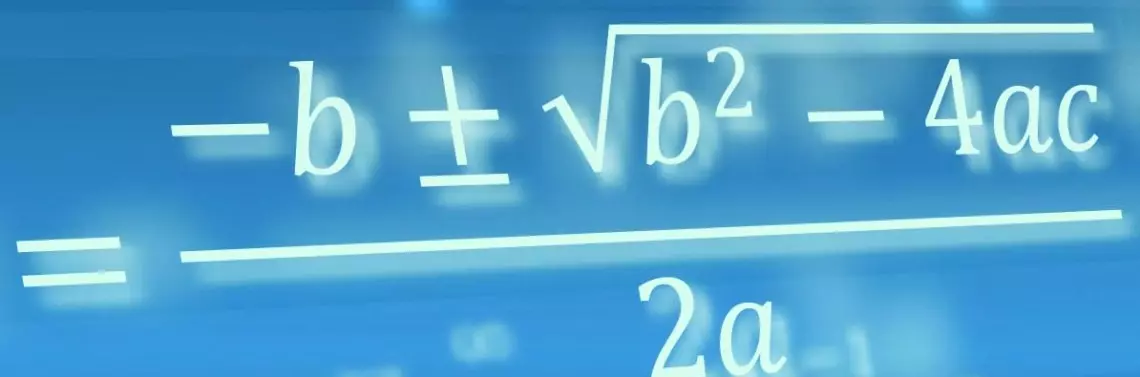Funkcje... Temat jakże abstrakcyjny dla naszych uczniów i trudny do pojęcia – szczególnie podczas pierwszych z nim zetknięć. Dotychczas podstawowe informacje na temat funkcji pojawiały się już w gimnazjum. W tym momencie musimy przygotować się na to, że za parę miesięcy naukę w szkołach ponadpodstawowych rozpoczną młodzi ludzie, którzy o funkcjach nigdy wcześniej nie słyszeli. Niestety, możliwość realizacji tego zagadnienia w ośmioklasowej szkole podstawowej istnieje tylko w ramach zajęć dodatkowych. Zatem w czasie nauki w szkole ponadpodstawowej uczeń będzie musiał dowiedzieć się w ogóle, czym są funkcje, poznać ich własności, a także zaznajomić się z wieloma konkretnymi przykładami i rodzajami funkcji. Niektóre własności funkcji możemy analizować ogólnie, dla wszystkich funkcji, inne są specyficzne tylko dla danego jej typu. Dlatego też w interaktywnych zasobach nauczyciela powinno znaleźć się miejsce zarówno na pliki dotyczące funkcji ogólnie, jak i te pokazujące przegląd własności poszczególnych jej rodzajów. Ja postaram się skupić na funkcji kwadratowej i pokazać jak najwięcej sposobów spojrzenia na to zagadnienie. Są to bowiem tematy kluczowe dla każdego ucznia przygotowującego się do matury – czy to na poziomie podstawowym, czy też rozszerzonym.
Pierwszym punktem będzie definicja funkcji kwadratowej i jej wzór. Oczywiście, możemy tworzyć wykresy dowolnych funkcji kwadratowych (i nie tylko) poprzez wpisanie ich konkretnego wzoru. Wystarczy jednak wprowadzić trzy suwaki: a, b, c, aby otrzymać możliwość generowania wzoru i wykresu dowolnej funkcji kwadratowej. W Widoku Algebry wpisujemy wówczas wzór: f(x) = ax^2 + bx + c. Po pojawieniu się wykresu i wzoru funkcji w nowej wersji GeoGebry dostępny będzie tam niebieski przycisk: PUNKTY SPECJALNE. Użycie go pozwoli w szybki sposób uzyskać miejsca zerowe i ekstrema funkcji, a także punkt przecięcia z osią y (ryc. 1).
POLECAMY

Użycie opisywanego przycisku znacznie ułatwia nam pracę. Wszystkie uzyskane punkty można, oczywiście, wyodrębnić samodzielnie, ale na pewno zajmie to trochę czasu.
Suwaki użyte podczas wykonywania rysunku możemy wyświetlić w oknie obok lub w tym samym oknie (w Widoku Grafiki 1 lub 2). Drugie okno również może stać się miejscem wyświetlania informacji na temat różnych postaci zapisywania wzoru funkcji kwadratowej (ryc. 2).

Opis taki uzyskamy jako odpowiednio sformułowane komentarze w postaci Tekstu. Niektóre z nich musimy stworzyć od początku sami, podczas gdy inne możemy wygenerować, wykorzystując polecenia GeoGebry. W Widoku Algebry możemy wpisać na przykład polecenie Postać Kanoniczna (f) i otrzymamy od razu interesujący nas zapis. Miejsca zerowe funkcji to współrzędne punktów A i B (zapis x(A), x(B)). Podobnie możemy uzyskać wielkości p i q. Oczywiście, powinniśmy dodatkowo zabezpieczyć nasz plik przed sytuacjami, kiedy funkcja ma tylko jedno miejsce zerowe lub nie ma ich wcale. W warunkach wyświetlania wybranych obiektów wystarczy wpisać nierówność d ≥ 0 albo d > 0 (gdzie d będzie oznaczało wielkość wyznacznika trójmianu). Taki plik może być oparciem podczas wprowadzania pojęcia funkcji kwadratowej, zapoznawania uczniów z kolejnymi postaciami jej zapisu, rozwiązywania zadań czy też przy lekcji powtórzeniowej. Jeżeli nasi uczniowie są zaznajomieni z programem GeoGebra, to wykonanie takiego pliku możemy również polecić im jako powtórzenie, utrwalenie wiadomości.
Na przygotowanej ilustracji możemy przedstawiać także różne własności funkcji kwadratowej i wspomagać się nim podczas rozwiązywania zadań na jej temat. Jeżeli dodatkowo wygenerujemy wykres funkcji ax2 i narysujemy wektor łączący wierzchołki obydwu paraboli, to otrzymamy rysunek doskonale ilustrujący zapis wzoru funkcji w postaci kanonicznej z przesunięciem o dany wektor (ryc. 3).

Opisywany plik może być też podstawą do innych aktywności. Dla przykładu weźmy zadania, w których porównujemy wartości dwóch funkcji – kwadratowej i dowolnej innej. W zadaniu takim mamy określić, kiedy wartości obu funkcji są takie same albo kiedy wartości jednej z nich są mniejsze/większe od wartości tej drugiej. Przykładem takiego zadania niech będzie graficzne rozwiązanie równania:
![]()
Aby otrzymać to rozwiązanie, wystarczy, że ustawimy odpowiednie wartości wielkości wyznaczanych przez suwaki dla funkcji kwadratowej, a następnie wprowadzimy wzór funkcji liniowej. Na rysunku otrzymamy wykresy obu funkcji i bez problemu odczytamy współrzędne punktów przecięcia ich wykresów (ryc. 4).

W podobny sposób możemy ilustrować rozwiązania nierówności, w których występować będzie trójmian kwadratowy. Dla uproszczenia pokażę to, bazując na powyższym równaniu. Jeżeli nierówność wyglądałaby tak:
![]()
to – zgodnie z oznaczeniami – wystarczy wpisać w Widoku Algebry formułę: f > r. Otrzymujemy wówczas rysunek odpowiedni dla interesującej nas nierówności (ryc. 5).

Zupełnie innym pomysłem na wykorzystanie pliku przygotowanego na samym początku jest pokazanie uczniom występowania zależności opisywanych za pomocą funkcji kwadratowej w praktyce. Przykłady kształtów paraboli lub zbliżonych do paraboli możemy odnaleźć bez problemu w otaczającym nas świecie. Aby połączyć to z wiedzą analityczną i zastosowaniem GeoGebry, wystarczy pobrać interesujący nas plik, a następnie umieścić go w obszarze roboczym programu (przy uruchomionym pliku z funkcją kwadratową). Służy do tego polecenie Obraz w menu programu. We właściwościach tak zaimportowanej grafiki możemy ustalić jej położenie, ustawić obraz jako tło (aby widoczny był układ współrzędnych i wszystkie wykresy), a także określić stopień nasycenia barw tak, aby rysunek był przede wszystkim czytelny. Umieszczając rysunek paraboli w tle, możemy polecić uczniom operowanie suwakami tak, aby – zmieniając współczynniki trójmianu – odnaleźli wzór lub chociaż przybliżony wzór opisujący funkcję kwadratową, której wykres przedstawia nasza ilustracja (ryc. 6).

Opisane przykłady pokazują, jak różnorodne może być wykorzystanie jednego pliku, który starannie wykonaliśmy na początku. Mówię o tym po to, aby przekonać wszystkich sceptyków, że praca z programem GeoGebra nie musi być trudna, a przygotowanie niektórych materiałów wcale nie jest pracochłonne.
Na koniec chciałabym jeszcze zwrócić uwagę na nieco inny przypadek. Chodzi o ilustrowanie zadań z parametrem. Do tego celu dla przejrzystości rysunku lepsze będzie przygotowanie nowego pliku. Niestety, nie będzie on już tak bardzo uniwersalny, ale łatwość jego wykonania przemawia za tym, że dla nikogo nie powinno być większym problemem zrobienie takiej ilustracji dla każdego z rozwiązywanych zadań. Dla przykładu weźmy zadanie polegające na badaniu liczby rozwiązań równania: (m + 3) x2 − 2 mx + m + 5 = 0 w zależności od wartości parametru m. Najpierw tworzymy suwak m, a następnie w Widoku Algebry wpisujemy wzór funkcji, dla której będziemy określać liczbę miejsc zerowych. Przy pracy z takim zadaniem warto zadbać o to, aby wartości graniczne parametru były większe niż domyślne (w moim przypadku wybrałam zakres od −20 do 10). Możemy też uruchomić animację dla wielkości zadawanej przez suwak, aby łatwiej nam było obserwować zmiany zachodzące na rysunku. Dodatkowo możemy wyznaczyć punkty przecięcia wykresu funkcji z osią x dla lepszej czytelności rysunku (ryc. 7).