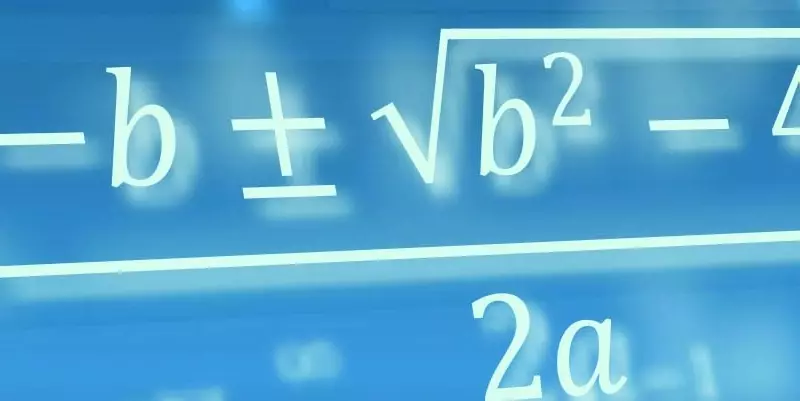W tym roku mieliśmy aż trzy egzaminy, w tym jeden zupełnie nowy zarówno dla uczniów, jak i dla nauczycieli. Ponieważ egzamin gimnazjalny przeszedł już do historii, a egzamin ósmoklasisty dopiero zaczął istnieć w szkolnej rzeczywistości i w związku z tym może jeszcze ewoluować, postanowiłam zatrzymać się chwilę nad zadaniami z arkusza maturalnego. Zawsze, kiedy przeglądam zadania, zastanawiam się, jak mogłoby wyglądać rozwiązywanie ich przy wykorzystaniu GeoGebry. Na początek chciałabym zwrócić uwagę na zadanie 29 z arkusza podstawowego tegorocznej matury (Ryc. 1).
Zazwyczaj jest tak, że na poziomie podstawowym autorzy zadań dołączają do nich gotowe rysunki. Ma to ułatwić rozwiązanie zadania uczniom, którzy mogą mieć problemy z samodzielnym stworzeniem modelu matematycznego.
Jednak zawsze, jeśli to możliwe, warto zrobić taki rysunek samodzielnie, nawet na kartce papieru. Przeanalizowanie przez ucznia zadania na pewno pozwoli mu lepiej je zrozumieć. Poza tym przy okazji wykonywania nowego rysunku możemy zasugerować, aby była to ilustracja spełniająca warunki zadania, ale zawierająca obiekty geometryczne w innym położeniu. Stworzenie własnej interpretacji może okazać się kluczowe na drodze poszukiwania rozwiązania. Jeszcze lepszym pomysłem byłoby stworzenie rysunku interaktywnego, który pozwala na przemieszczanie obiektów i różnorodne obserwacje i pomiary. Nowa ilustracja mogłaby wyglądać tak jak na ryc. 2.
POLECAMY


Zaznaczone zostały kąty, o których jest mowa w zadaniu, oraz podana jest ich miara. Możemy także wykonać proste obliczenie – stosunek miary kąta ASD do miary kąta BCS. Podczas poruszania punktami wykorzystanymi do wykonania konstrukcji widoczne będzie wówczas, że liczba ta jest stała i zawsze wynosi 3.
Dla ułatwienia dowodu tego faktu możemy jeszcze zaznaczyć odpowiednie kąty, których miary są sobie równe (ryc. 3).

Obserwując rysunek, łatwo zauważyć zależności pomiędzy miarami poszczególnych kątów, wynikające z własności miar kątów w trójkątach. Dodatkowo możemy także stwierdzić, że kąty zaznaczone kolorem ciemnoszarym (ABS, BAS) są dwa razy większe od kątów zaznaczonych kolorem jasnoszarym (BCS, BSC). Wtedy już łatwo wywnioskować, że suma miar kątów – BSC i ASD – jest równa czterokrotności kąta BSC, a co za tym idzie, kąt ASD jest jego trzykrotnością. Zadanie to jest warte uwagi jeszcze z jednego powodu. Mimo iż pochodzi z arkusza maturalnego, to poziom wiedzy, jaką należy posiadać do sformułowania uzasadnienia, nie wybiega poza program szkoły podstawowej. Dlatego też bez problemu możemy to zadanie wykorzystać podczas lekcji z młodszymi uczniami. Gotową ilustrację do zadania można znaleźć pod kodem poniżej.

Podczas gdy w arkuszu maturalnym na poziomie podstawowym zadania są zazwyczaj zaopatrzone w rysunki, nieco inaczej sprawa wygląda w przypadku zadań z arkusza poziomu rozszerzonego. Tam gotowe ilustracje pojawiają się rzadziej, bowiem to od uczniów wymagamy odpowiednio wykształconej wyobraźni matematycznej i umiejętności stworzenia odpowiedniego modelu. Przykładem może być zadanie 9 z tegorocznego arkusza matury rozszerzonej.
Wykonanie rysunku ilustrującego warunki zadania jest stosunkowo proste i nie powinno sprawić problemu średnio zaawansowanemu użytkownikowi GeoGebry. Dla pozostałych zamieszczam link do gotowego rysunku: //www.geogebra.org/graphing/ubedrrby (ryc. 4).


Dodam jedynie, że przy tworzeniu trójkąta równoramiennego ABC dla potrzeb zadania lepiej będzie zacząć od odcinka AB i jego symetralnej, na której wybierzemy punkt C. Tradycyjnie stosowana konstrukcja wykorzystująca przecinające się łuki okręgów może okazać się w tym przypadku nieco kłopotliwa. Poza tym zastosowanie jej uniemożliwi nam swobodne poruszanie punktem C, plik stanie się trudny w użyciu. Na przedstawionej przeze mnie ilustracji poruszać możemy swobodnie punktami A i B oraz w znacznym stopniu punktem C.
Pomimo iż jest to zadanie z poziomu rozszerzonego matury, to po wykonaniu rysunku samo uzasadnienie mogą przedstawić również uczniowie realizujący poziom podstawowy, a także niektórzy młodsi uczniowie. Mamy ogromną paletę możliwości szukania i formułowania dowodu. Możemy opierać się na przystawaniu i podobieństwie trójkątów, twierdzeniu Talesa czy też funkcjach trygonometrycznych. Rysunek interaktywny daje nam możliwość rozpatrzenia na początku przypadków szczególnych. W warunkach zadania jest zastrzeżenie, że punkty A i M nie mogą się pokrywać. Jednak kiedy na naszym rysunku w GeoGebrze zastosujemy takie ustawienie, możemy od razu zobaczyć, jak wyglądają interesujące nas odcinki, i widzimy, że przypadek jest trywialny (ryc. 5).

Na naszej ilustracji możemy w dowolnym miejscu dorysowywać niezbędne do dowodu proste i odcinki. Na przykład rysując symetralną odcinka AB i odcinki do niej prostopadłe, przechodzące przez punkty M i N, mamy podział na łatwe do zauważenia trójkąty przystające, skąd w prosty sposób przejdziemy do długości interesujących nas odcinków (ryc. 6).


Poza zadaniami „na dowodzenie” GeoGebra doskonale nadaje się do wykorzystania także podczas zadań, w których mamy wykonać konkretne obliczenia. Pozwala w prosty sposób odnaleźć interesujące nas obiekty, jeszcze przed wykonaniem działań, a także daje możliwość sprawdzenia poprawności uzyskanego wyniku. Przykładem takiego zadania może być zadanie 33 z arkusza matury poziomu podstawowego.
Do wykonania ilustracji do tego zadania możemy włączyć widoczność układu współrzędnych oraz siatki. Po wprowadzeniu wielkości podanych w zadaniu – współrzędnych punktu A oraz równania prostej y – możemy zacząć poszukiwania punktu B i jego współrzędnych. Kroki, jakie w tym celu poczynimy, nie doprowadzą nas tym razem do rozwiązania, ale mogą pokazać jedną z dróg, jaką należy podążać, aby je odnaleźć. Kreślimy prostą prostopadłą do danej prostej, przechodzącą przez punkt A. Następnie rysujemy okrąg, dzięki któremu odnajdujemy punkt B (ryc. 7).

Oczywiście, zamiast okręgu moglibyśmy narysować odpowiednie wektory albo szukać jeszcze innych sposobów. Chodzi jednak o zaobserwowanie, jak GeoGebra podpowie nam, jakie obliczenia wykonać. Szukamy najpierw równania prostej prostopadłej do prostej y = 3x, przechodzącej przez punkt A. Potem odnajdujemy współrzędne punktu przecięcia obydwu prostych (punktu P). Na koniec możemy wykorzystać równanie okręgu, rachunek wektorowy albo wzór na środek odcinka i w ten sposób otrzymamy końcowe rozwiązanie. Dobrze się składa, że współrzędne zarówno punktu P, jak i punktu B nie są całkowite. Unikniemy bowiem pokusy, aby po odczytaniu ich współrzędnych w oknie programu zaniechać poszukiwania rozwiązania. Na tym przykładzie widać, że powinniśmy wykonać obliczenia, których wyniki możemy porównać z odczytanymi z rysunku wartościami. Program komputerowy nas prowadzi, podpowiada nam, pomaga, ale nie wyręcza nas, a na pewno nigdy nie zwalnia z myślenia.