W nauczaniu matematyki znajdują się tematy, które pojawiają się tylko na chwilę i takie, które powracają jak bumerang. Są takie własności liczb czy figur geometrycznych, bez których nie uda nam się wprowadzić bardziej złożonych pojęć lub wykonać bardziej skomplikowanych obliczeń. Są zagadnienia uniwersalne, jest wiedza, którą uczniowie powinni mieć w głowie o każdej porze, abyśmy mogli w odpowiednim momencie odwołać się do niej i ją wykorzystać. Wśród takich zagadnień są z pewnością wzory opisujące sposób obliczania pól powierzchni różnych figur płaskich.
Matematycznych programów komputerowych możemy używać podczas naszych lekcji przy różnych okazjach. Będą one przydatne zarówno podczas wprowadzania nowych treści, jak i utrwalania zdobytej już wiedzy. Dlatego też polecam włączenie GeoGebry w proces przygotowań do różnego typu konkursów i egzaminów zewnętrznych.
Ogromna wszechstronność zastosowań GeoGebry to fakt, który dla jej licznych użytkowników jest oczywisty i niepodważalny. Jednak trzeba przyznać, że stosunkowo rzadko mówi się o wykorzystaniu arkusza kalkulacyjnego, który jest dołączony do programu. Dlatego też stwierdziłam, że warto poświęcić mu nieco więcej uwagi.
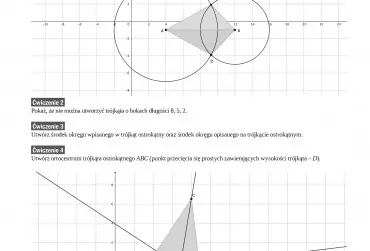
Jakie miejsce zajmują obecnie konstrukcje geometryczne w nauczaniu matematyki? Myślę, że trudno udzielić na to pytanie jednoznacznej odpowiedzi. Na pewno dużo zależy od indywidualnego podejścia nauczyciela i nacisku kładzionego przez niego na ten element edukacji matematycznej, jakim jest umiejętność wykonywania konstrukcji.
Chociaż zagadnienia związane z wektorami zostały przypisane do poziomu rozszerzonego wymagań maturalnych, to wielu nauczycieli decyduje się wprowadzić podstawy tego tematu we wszystkich swoich klasach.
Nie są to bowiem treści nazbyt skomplikowane, a ich znajomość może ułatwić omawianie innych tematów (na przykład związanych z przekształceniami wykresów funkcji). Ponadto z pojęciem wektora uczniowie mogą mieć styczność na innych przedmiotach, dlatego warto pokazać im matematyczne podejście do tego tematu, jeśli tylko mamy taką możliwość.
Mimo tego, że twierdzenie Talesa to zagadnienie dość proste, w trakcie licznych zmian podstawy programowej było ono „przesuwane” na dalsze etapy edukacyjne, aż w końcu całościowo znalazło się wśród zagadnień dla szkoły ponadgimnazjalnej. Mając jednak jakiekolwiek godziny do dyspozycji dla nauczyciela, możemy także bez problemu zdecydować się na omówienie tego twierdzenia już wcześniej (zarówno w klasie drugiej i trzeciej obecnego gimnazjum, jak i w klasach siódmej i ósmej nowej szkoły podstawowej). W każdym przypadku warto wyposażyć się w przydatne narzędzia, które pozwolą nam sprawnie to twierdzenie omówić.
Jeżeli będziemy analizować listę zdefiniowanych funkcji dostępnych w programie GeoGebra, to z pewnością wielu z nas będzie usatysfakcjonowanych, ponieważ znajdziemy tam wiele przydatnych poleceń gotowych do użycia. Wśród nich znajdziemy między innymi całą kolekcję funkcji trygonometrycznych, hiperbolicznych i funkcji do nich odwrotnych. Poza tym mamy możliwość wykonywania dowolnego potęgowania, obliczania silni czy też wartości bezwzględnej. Niestety, nieco inaczej sprawa wygląda w przypadku logarytmów.
GeoGebra jest programem, a właściwie można byłoby powiedzieć – projektem stale rozwijającym się i zmieniającym. Dzięki temu jej rozwój podąża za współczesnymi trendami. Od dawna mamy możliwość korzystania z programu w wersji mobilnej, na urządzenia przenośne. Możemy uruchomić program w przeglądarce, bez konieczności instalowania go na komputerze. Praca z GeoGebrą możliwa jest zatem na smartfonach i tabletach, a także na każdym komputerze posiadającym dostęp do Internetu.
Wśród zagadnień omawianych w szkole na lekcjach matematyki znajdziemy takie, które potocznie nazwać możemy przekrojowymi, czyli takimi, które nie dają się przypisać do jednego, konkretnego etapu edukacyjnego. Poza tym musimy pamiętać, że pojęcia matematyczne są kształtowane niejednokrotnie przez długi czas i zaczynamy o nich mówić czasem dużo wcześniej, zanim uczniowie poznają ich właściwą definicję.
GeoGebra to niezmiennie doskonałe narzędzie do ilustrowania pojęć geometrycznych na każdym poziomie nauczania, dlatego pomimo mnogości zastosowań programu warto wracać do tych zagadnień. Ponadto najnowsza wersja GeoGebry pozwala na wyświetlenie w prosty sposób tylko geometrycznych narzędzi, co może znacznie ułatwić pracę.
