Geometria Mikołaja Kopernika:

Mikołaj Kopernik - księgi

Jego notatki pochodzące z około 1520 roku są najstarszym śladem posługiwania się funkcją trygonometryczną secans. Kopernik wprowadził tę funkcję, a później przygotował tablice trygonometryczne jej wartości. Tablice te stanowiły uzupełnienie tablic Tabulae directionum Regiomontanusa (1436–1476).

Teorię heliocentryczną Kopernik omówił w dziele zatytułowanym Nicolai Copernici Torinensis De Revolutionibus orbium coelestium, Libri VI [Mikołaja Kopernika Toruńczyka o obrotach ciał niebieskich, ksiąg VI]1. Za podstawę wszelkich rozważań posłużyły mu tam geometria płaska i sferyczna. Wykorzystywał Elementy Euklidesa oraz rachunki Ptolemeusza związane z rozwiązywaniem trójkątów płaskich i sferycznych. Kopernik w De Revolutionibus rozbudował teorię Ptolemeusza i wzbogacił ją o sposoby obliczania cięciwy stowarzyszonej z dowolnym łukiem okręgu oraz cięciwy przeciwległej kątowi, którego łuk jest dany. Ponadto sformułował i udowodnił twierdzenie sinusów (to twierdzenie jest jego najważniejszym odkryciem matematycznym). Cały materiał geometryczny, na którym Kopernik oparł rozważania na temat heliocentryzmu, umieścił w trzech rozdziałach pierwszej księgi De Revolutionibus, tj. rozdziałach XII (pt. O cięciwach w kole), XIII (O bokach i kątach trójkątów płaskich prostolinijnych) i XIV (O trójkątach sferycznych)2. W rozdziale XII autor zajął się opisaniem korelacji pomiędzy łukiem koła, kątem środkowym opartym na tym łuku, cięciwą z nimi stowarzyszoną oraz promieniem koła. Pozwoliło to, znając niektóre spośród tych wartości, obliczyć pozostałe. Rozdział XIII poświęcił na omówienie sposobów rozwiązywania trójkątów płaskich, a rozdział XIV – na rozwiązywanie trójkątów sferycznych.

W niniejszym artykule dokonamy analizy treści zawartych w XII rozdziale I księgi De Revolutionibus. Praca ta otwiera serię artykułów poświęconych matematyce Mikołaja Kopernika.

Dzieło De Revolutionibus było już wielokrotnie badane przez naukowców. Tutaj pokusimy się o jego analizę z bardziej współczesnego punktu widzenia. Zachowana zostanie struktura oryginału, omówione zostaną wszystkie treści w nim zawarte, jednakże będą one uzupełnione o dodatkowe wyjaśnienia, dowody, a nawet uogólnienia. Użyte też będą współczesne oznaczenia, a niekiedy również współczesna terminologia.
Takie podejście do dzieła Kopernika ma na celu uczynienie go bardziej przystępnym dla współczesnych odbiorców oraz pokazanie, że teoria geometryczna kryjąca się za odkryciem heliocentryzmu nie była skomplikowana.

O obrotach ciał niebieskich - Mikołaj Kopernik

De Revolutionibus Mikołaja Kopernika w całości po raz pierwszy zostało opublikowane w 1543 roku i nosiło tytuł Nicolai Copernici Torinensis De Revolutionibus orbium coelestium, Libri VI [Mikołaja Kopernika Toruńczyka o obrotach ciał niebieskich, ksiąg VI]1. Jak wskazuje tytuł, autor podzielił swój wykład na sześć części. W pierwszej z nich zajął się opisaniem położenia wszystkich planet, ze szczególną uwagą poświęconą analizie ruchów Ziemi, w kolejnych częściach porównał te ruchy z ruchami innych planet i pozostałych sfer niebieskich, a wysunięte wnioski pozwoliły mu na dokładne wyjaśnienie systemu wszechświata.

Księgę I rozpoczął od uzasadnień, iż świat jest kulisty, niezmierzony i podobny do nieskończonego, a także, że wszystko zawierająca w sobie sfera gwiazd jest nieruchoma, wszystkie zaś inne ciała niebieskie poruszają się po kołach3, również Ziemia porusza się pewnymi ruchami kolistymi. Wstęp ten miał stanowić fundament całej astronomii.

Pisząc swoje dzieło, Kopernik opierał się na geometrii płaskiej i sferycznej. Na tę bazę matematyczną zarezerwował trzy rozdziały (XII, XIII i XIV) księgi I. Wyraźnie podkreślił wówczas, że owa wiedza geometryczna służyła mu za bazę do wszelkich rachunków.

Mikołaj Kopernik - postrzeganie przez współczesnych matematyków

Te trzy rozdziały okazały się bardzo wartościowe dla matematyków. Po tym, jak Tydeman Gize, biskup chełmiński, a prywatnie przyjaciel Kopernika przygotowujący do wydania jego dzieło o obrotach ciał niebieskich (Kopernik nie mógł tego uczynić własnoręcznie ze względu na chorobę), pokazał rękopis profesorowi Joachimowi Retykowi z Wittenbergi, ten niezwłocznie wystosował list do Jerzego Hartmana z Norymbergii z prośbą o publikację części geometrycznej. Nastąpiło to w 1542 roku, czyli rok przed wydaniem całego dzieła.

Opublikowana praca składała się z 28 kart. Wstęp do niej stanowiła przedmowa Retyka do Hartmana z prośbą o wydanie pracy drukiem i uzasadnieniem jej wagi naukowej. Pojawiło się tutaj stwierdzenie: cała architektura z geometryi powstała4, a następnie: Wiadomo ci [Hartmanowi], że nauka o trójkątach bardzo rozległe ma zastosowanie w różnych gałęziach matematyki, a głównie w astronomii4.
Przedmowę Retyka zakończył apel do młodzieży5:

Szkolna młodzieży! Od pierwszych lat ucz się tej 
umiejętności,
Która z miarami i liczbami obznajmia;
Wielkie bowiem nagrody odniesiesz za podjętą pracę.
Pismo to wskazuje ci drogę do nieba,
Gdzie się cudowny świat rozciąga w niezmiernych 
przestworach,
Jeżeli myślą zechcesz sięgnąć ich granic.
Albo w jakiej okolicy nieba gwiazdy się błąkają,
I jakie są drogi odwiecznych biegów;
Dlaczego księżyc towarzysza mgłą ciemną osłania,
A on księżycowi użytku światła odmawia;
Lub jakie losy kierują przyszłością;
Jakie klęski niosą ludom gwiazdy nieprzyjazne.
To jeśli wiedzieć pragniesz, pierwej znać trzeba naukę, 
Które wyłożą ci w treści te początki.
A gdy myśli ludzkie, co biorą zaród z nieba,
Zbłąkają się daleko od ojczystego siedliska,
Ta nauka oswobodziwszy je z brzmienia ziemskości,
Napowrót do niebieskiego pałacu zanosi.

Dalej omówiona została trygonometria płaska (na dwóch kartach), trygonometria sferyczna (na sześciu kartach), a najobszerniejszą jej część stanowiły tablice połówek cięciw odpowiadających łukom o miarach od 0° do 90° przy postępie minutowym (dziewiętnaście kart).

Cięciwa koła – analiza XII rozdziału księgi I De Revolutionibus

W dalszej części niniejszego artykułu zostanie zaprezentowany i przeanalizowany materiał zawarty w rozdziale  XII księgi I De Revolutionibus6. Zostaną tutaj użyte współczesne oznaczenia i terminologia.
Podstawowe różnice dotyczące oznaczeń i terminologii będą następujące:

• Kopernik nie używał sformułowania „równe w przybliżeniu”; do końca XIX wieku między wielkościami, które różniły się od siebie nieznacznie, pisano znak równości; w niniejszej analizie, jeżeli dwie wielkości będą różniły się od siebie nieznacznie, będziemy pisali: „równe w przybliżeniu”, „równe około” itp. (symbolicznie: „≈”);
• Kopernik pisał: „kąt ABC jest równy…”; w XXI wieku używamy pojęcia miary kąta: „miara kąta ABC wynosi…” (symbolicznie: |ABC| = …);
• u Kopernika pod pojęciem „linii” kryły się zarówno dzisiejsze proste, jak i odcinki; w przeprowadzonej poniżej analizie będziemy używali pojęć: prosta oraz odcinek (długość odcinka AB będziemy zapisywali symbolicznie: |AB|, tego symbolu nie używał Kopernik);
• w niektórych dowodach, które będą tutaj przeprowadzone i jednocześnie będą uzupełnieniami dzieła Kopernika, zostanie użyte pojęcie równoważności zdań (to, iż zdania p oraz q są równoważne, zapisuje się symbolicznie: p ⇔ q); tym pojęciem Kopernik się nie posługiwał.

Długości boków - wielokąty foremne

Jak już zostało wspomniane, w rozdziale XII Kopernik omówił zależność pomiędzy łukiem okręgu, kątem środkowym opartym na tym łuku, cięciwą z nimi stowarzyszoną oraz promieniem okręgu. Pokazał, że jeżeli niektóre z tych wielkości są znane, to można obliczyć pozostałe. W swoich rozważaniach Kopernik korzystał z następującej uwagi:

W dalszej części Kopernik podał wartości długości boków wielokątów foremnych wpisanych w koło o promieniu 100 000. Mianowicie bok odpowiednio: trójkąta, czworokąta, pięciokąta, sześciokąta i dziesięciokąta foremnego wpisanego w koło o promieniu 100 000 jest równy długości cięciwy stowarzyszonej z łukiem odpowiednio: 120°, 90°, 72°, 60°, 36°; co, po obliczeniu, daje nam odpowiednie długości boków: 173 205, 141 422, 117 557, 100 000, 61 803.

Powyższa uwaga nie została przez Kopernika uzasadniona. Zauważmy, że podane wyżej wartości długości boków są tak naprawdę wartościami przybliżonymi; w podobnych sytuacjach, w dalszej analizie, będziemy wyraźnie zaznaczać, że są to wartości przybliżone.
Postaramy się teraz udowodnić powyższe stwierdzenie. Przedstawimy rachunki prowadzące do wyliczenia długości każdego z boków tych wielokątów, z tym że wielokąty te wpisane zostaną w koło o dowolnym promieniu r. Długości zostaną wyznaczone w sposób dokładny, przy czym, aby nie odbiegać w znaczny sposób od rachunków Kopernika, za każdym razem podana będzie również przybliżona wartość długości boku.

W całej niniejszej analizie przyjmujemy, że promień koła jest równy r, podczas gdy Kopernik w swoim dziele za każdym razem rozważał koło o promieniu 100 000. 

Długość boku - trójkąt równoboczny

Zauważmy, że mając trójkąt równoboczny wpisany w okrąg, możemy ustalić zależność pomiędzy bokiem tego trójkąta a promieniem okręgu. Każdy z boków trójkąta jest podstawą innego trójkąta – o wierzchołku w środku okręgu i kącie przy tym wierzchołku równym 120° (360° : 3 = 120°).          

 Na powyższym rysunku jeden z tych trójkątów został oznaczony jako ABO. Trójkąt ABO jest trójkątem równoramiennym. Długości jego ramion, |AO| oraz |BO|, są równe długości promienia okręgu, czyli r. Długość jego podstawy, czyli |AB|, została oznaczona a.
W związku z tym, że ABO jest trójkątem równoramiennym, zatem |<OAB| = |<OBA| = 30°. Ponadto pole tego trójkąta jest równe:

ale z drugiej strony wynosi ono:

Zatem:

czyli:

Stąd:

Czyli długość cięciwy AB, to:

co w przybliżeniu daje nam 1,73205r. Zauważmy, że kwadrat długości boku trójkąta równobocznego jest równy potrojonemu kwadratowi promienia.

Długość boku kwadratu

Podobnie stosunek długości boku kwadratu do promienia okręgu, w który został on wpisany, to:

Zatem długość boku kwadratu to w przybliżeniu 1,41422r oraz długość cięciwy stowarzyszonej z łukiem 90° to w przybliżeniu 1,41422r. Zauważmy, że kwadrat boku kwadratu jest równy podwojonemu kwadratowi promienia okręgu, w który został wpisany.

Długość boku - pięciokąt foremny

Stosunek długości boku pięciokąta foremnego wpisanego w okrąg do promienia tego okręgu, to:

zatem:

czyli długość boku pięciokąta foremnego wpisanego w okrąg o promieniu r i jednocześnie długość cięciwy stowarzyszonej z łukiem 72°, będącym częścią okręgu o promieniu r, to w przybliżeniu 1,17557r.

Długość boku - sześciokąt foremny

Stosunek długości boku sześciokąta foremnego do promienia okręgu, w który został on wpisany, to:

zatem bok tego sześciokąta jest równy promieniowi okręgu opisanego na tym sześciokącie. Tym samym długość cięciwy stowarzyszonej z łukiem 60° będącym częścią okręgu o promieniu r to r.

Długość boku dziesięciokąta foremnego

Zależność pomiędzy bokiem dziesięciokąta foremnego wpisanego w okrąg o promieniu r a promieniem tego okręgu jest następująca:

zatem bok dziesięciokąta foremnego wpisanego w okrąg o promieniu r jest równy w przybliżeniu 0,61803r. Tym samym długość cięciwy stowarzyszonej z łukiem 36° to w przybliżeniu 0,61803r.

Zależność między bokami pięciokąta i dziesięciokąta foremnego

Po podaniu długości boków wielokątów foremnych Kopernik określił zależność pomiędzy długościami boków pięciokąta i dziesięciokąta foremnego, gdy oba zostały wpisane w ten sam okrąg. Zależność tę charakteryzuje następujące twierdzenie:

Twierdzenie: Kwadrat boku pięciokąta foremnego wpisanego w okrąg jest równy sumie kwadratów boku dziesięciokąta foremnego wpisanego w ten sam okrąg i promienia tego okręgu.
Autor pozostawił to twierdzenie bez dowodu. Tutaj zostanie to uzupełnione.

Wprowadźmy oznaczenia:

• a – bok pięciokąta foremnego,
• b – bok dziesięciokąta foremnego,
• r – promień okręgu, w który zostały wpisane pięciokąt i dziesięciokąt.

Zauważmy, że zgodnie z rachunkami umieszczonymi w poprzednich punktach prawdziwe są następujące równości:

W związku z tym, aby wykazać prawdziwość powyższego twierdzenia, należy udowodnić, że:

Dowód:
Dowód przeprowadzimy, korzystając z metody przejść równoważnych:

Jasne jest, że zdanie 1 = 1 jest prawdziwe. Ponadto wszystkie przejścia, których dokonaliśmy, były równoważnościami. 
Zatem zdanie:

też musi być prawdziwe, co kończy dowód.■
Tym samym zostało udowodnione, że kwadrat boku pięciokąta foremnego wpisanego w okrąg jest równy sumie kwadratów boku dziesięciokąta foremnego wpisanego w ten sam okrąg i jego promienia.

Obliczanie długości - cięciwa okręgu

Cięciwy stowarzyszone z łukami uzupełniającymi się do półokręgu

Dalej Kopernik zauważa, że jeżeli znana jest cięciwa stowarzyszona z pewnym łukiem, to można obliczyć długość cięciwy stowarzyszonej z łukiem uzupełniającym poprzedni łuk do półokręgu. W tym przypadku suma kwadratów obu cięciw będzie równa kwadratowi średnicy okręgu (na podstawie twierdzenia: każdy kąt wpisany w okrąg i oparty na średnicy jest kątem prostym).
Podaje również dwa przykłady, w których oblicza:

• długość cięciwy stowarzyszonej z łukiem 144°: skoro z łukiem 36° stowarzyszona jest cięciwa o długości w przybliżeniu 0,61803r, zatem cięciwa stowarzyszona z łukiem 144° jest równa w przybliżeniu:

• długość cięciwy stowarzyszonej z łukiem 108°: skoro znamy długość cięciwy stowarzyszonej z łukiem 72°, zatem cięciwa stowarzyszona z łukiem 108° ma długość równą w przybliżeniu:

Cięciwa stowarzyszona z różnicą dwóch łuków

Nieco więcej uwagi astronom poświęca wyjaśnieniu, w jaki sposób, znając cięciwy dwóch łuków, można znaleźć cięciwę stowarzyszoną z różnicą tych łuków. Kluczem jest tutaj twierdzenie Ptolemeusza.

Twierdzenie Ptolemeusza

Iloczyn długości przekątnych czworokąta wpisanego w okrąg jest równy sumie iloczynów długości przeciwległych boków tego czworokąta (dowód tego twierdzenia, przeprowadzony przez Mikołaja Kopernika, można znaleźć w § 232 podręcznika do planimetrii Karla Koppego7).

Istotnie, niech dane będą długości cięciw przynależnych łukom AB oraz AC – obliczymy długość cięciwy stowarzyszonej z łukiem BC 
(będącym różnicą dwóch wcześniejszych):

gdzie AD jest średnicą okręgu.
Zauważmy, że łuki AC oraz CD tworzą razem półokrąg, zatem:

Z tego samego powodu:

Tym samym znamy długości cięciw AB, AC, CD, BD oraz średnicę AD, możemy więc skorzystać z twierdzenia Ptolemeusza i obliczyć długość cięciwy BC: 

Uwaga: Przeprowadzając analogiczne rozumowanie dla łuków 72° i 60°, których cięciwy wyliczyliśmy powyżej, bez trudu można pokazać, że z łukiem 12° stowarzyszona jest cięciwa o długości równej w przybliżeniu 0,20905r.

Cięciwa stowarzyszona z połową łuku

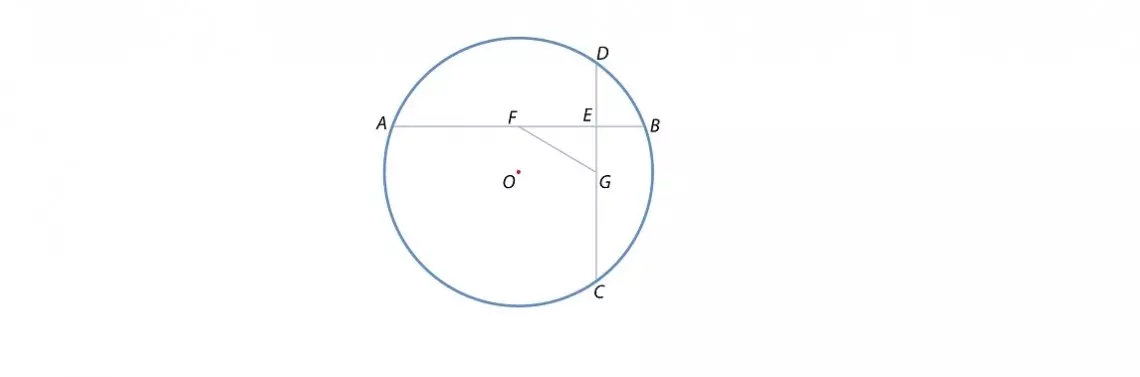
Kolejny akapit rozdziału to odpowiedź na pytanie: Jeżeli znana jest cięciwa stowarzyszona z pewnym łukiem, to w jaki sposób można obliczyć cięciwę odpowiadającą połowie tego łuku? Istotnie, rozważmy sytuację przedstawioną na rysunku:

Niech dany będzie odcinek BC, czyli cięciwa stowarzyszona z łukiem BC.
Sposób, dzięki któremu można znaleźć długość cięciwy odpowiadającej połowie tego łuku, jest następujący:

1. Przez środek okręgu, czyli punkt E, prowadzimy prostą prostopadłą do cięciwy BC. Punkt przecięcia tej prostej z cięciwą oznaczamy F, a jej punkty przecięcia z okręgiem – G oraz D w ten sposób, że punkt D leży na łuku BC. Wówczas każdy z łuków BD oraz DC jest połową łuku BC. 
2. Następnie kreślimy dwie średnice – jedną przechodzącą przez punkt D (jej drugi koniec oznaczamy G), drugą przechodzącą przez C (jej drugi koniec oznaczamy A).
3. Rozważmy teraz ABC oraz EFC. Zauważmy, że punkt E dzieli AC na połowę oraz F dzieli BC na połowę, zatem EF || AB, a tym samym:

4. W związku z tym, że znamy długość cięciwy BC, bez trudu możemy obliczyć długość cięciwy AB (ponieważ łuki oparte na tych cięciwach uzupełniają się do półokręgu), a sposób obliczenia był omówiony wcześniej. Zatem z (*) możemy obliczyć też długość odcinka EF. Znając |EF|, bez trudu możemy obliczyć również |DF| – jest to różnica promienia okręgu i |EF|. 
5. Rozważmy teraz trójkąt DBG. Kąt GBD jest kątem wpisanym, opartym na średnicy, zatem jest on kątem prostym. Czyli DBG jest prostokątny. Zauważmy również, że BFD oraz GFB są prostokątne, zatem korzystając z twierdzenia Pitagorasa, otrzymujemy następujący układ równań:

który możemy zapisać w sposób równoważny następująco:

stąd:

Z powyższej równości otrzymujemy, że:

czyli:

Tym samym kwadrat długości cięciwy BD jest równy iloczynowi długości odcinka DF i średnicy DG.
Dalej autor podał przykłady: z łukami 6°, 3°, 1 1/2°, 3/4° stowarzyszone są cięciwy o długościach 10 467, 5235, 2618, 1309. Zapisując wynik Kopernika w zgodzie z notacją przyjętą w niniejszej analizie, mamy, iż: z łukami 6°, 3°, 1 1/2°, 3/4° stowarzyszone są cięciwy o długościach równych w przybliżeniu 0,10467r, 0,05235r, 0,02618r, 0,01309r. Przeprowadźmy tutaj rachunki pozwalające wyznaczyć przybliżone wartości długości cięciw stowarzyszonych z łukami 6°, 3°, 1 1/2°, 3/4°. Same długości cięciw podamy tutaj z większą dokładnością. Ta większa dokładność będzie bardzo istotna dla rozważań, które zostaną umieszczone w podpunkcie 3.2.5.

Przykłady:
Niech dany będzie łuk 12°. Wcześniej zauważyliśmy, że cięciwa odpowiadająca temu łukowi ma długość równą w przybliżeniu 0,2095r (oznaczmy ją tak, jak w powyższym przypadku ogólnym, czyli |BC|). Stosując powyższe rozumowanie, w naszej konkretnej sytuacji otrzymujemy:

stąd:

czyli:

W związku z tym długość cięciwy stowarzyszonej z łukiem 6° jest taka, że:

zatem:

Podobnie można obliczyć, że łukowi 3° odpowiada cięciwa, której długość wynosi w przybliżeniu:

oraz że łukom 1°, ° odpowiadają cięciwy równe w przybliżeniu 0,0261782r, 0,0130894r.

Cięciwa stowarzyszona z sumą łuków

Kopernik kontynuuje rozważania w sposób następujący: Znając długości cięciw odpowiadających dwóm łukom, możemy obliczyć długość cięciwy odpowiadającej sumie tych łuków. Niech dane będą długości cięciw AB oraz BC. Łuk AC jest wówczas sumą łuków AB oraz BC:

Niech F będzie środkiem koła. Narysujmy dwie średnice, jedną przechodzącą przez punkt A (o drugim końcu D), drugą przechodzącą przez punkt B (o drugim końcu E). W związku z tym, że znamy długości cięciw AB i BC, bez trudu możemy obliczyć też długości cięciw BD oraz CE. Ponadto zauważmy, że |AB| = |ED|. Zatem w czworokącie BCDE znamy długości boków BC, BE, ED oraz obie jego przekątne, czyli |BD| oraz |CE|. Korzystając z twierdzenia Ptolemeusza, bez trudu można wyliczyć wówczas |CD|. W związku z tym, że łuk CD razem z łukiem AC tworzą półkole, zatem na mocy 3.2.1. można wyliczyć długość cięciwy AC. 
Po czym formułuje wniosek:

Wniosek: 
Mając daną miarę łuku, z łatwością można obliczyć długość cięciwy odpowiadającej temu łukowi powiększonemu o 3/4° (przypomnijmy, że łukowi 3/4° odpowiada cięciwa długości równej w przybliżeniu 0,0130894r). 
oraz uwagę:
Uwaga: Łukowi 1° odpowiada cięciwa o długości około
0,0130894r · 4/3  = 0,0174525r, 
tym samym mając dany łuk, możemy policzyć przybliżoną długość cięciwy stowarzyszonej z łukiem powiększonym o 1°.

Twierdzenie o łukach i stowarzyszonych z nimi cięciwach

Dalej autor dowodzi następujące twierdzenie: 
Jeżeli dane są długości dwóch różnych łuków, z których każda jest mniejsza od 1/4 długości okręgu, wówczas stosunek długości większego łuku do mniejszego jest większy niż stosunek odpowiadających im cięciw.

Przed przystąpieniem do dowodu, a później omówienia twierdzenia czyni krótkie przygotowanie: rozważmy łuk ABC podzielony przez punkt B w taki sposób, że |BC|1 > |BA|1.

Wówczas, aby udowodnić twierdzenie, należy wykazać, że:

Dowód:
W pierwszym kroku dowodu poprowadźmy cięciwę, która połowi ABC – cięciwę BD. Wówczas |AD| = |CD|, zatem ADC jest równoramienny. Jeżeli poprowadzimy teraz prostopadłą do podstawy AC z punktu B i oznaczymy punkt przecięcia tej prostej i podstawy jako F, to |AF| = |FC|. Ponadto, zgodnie z twierdzeniem o dwusiecznej:

Z założenia wiemy, iż |BC|1 > |BA|1, zatem |BC|c > |BA|c. Stąd na podstawie powyższej proporcji: |EC| > |EA|. Tak więc punkt F leży na odcinku EC oraz, przypomnijmy, DF jest prostopadły do AC, czyli |DA| > |DE| > |DF|. Jeżeli poprowadzimy teraz okrąg o środku w punkcie D i promieniu |DE| oraz punkt przecięcia tego okręgu z AC oznaczymy H, a jego punkt przecięcia z (przedłużeniem) DF oznaczymy I, to punkt H musi leżeć pomiędzy D i A, a punkt I leży na przedłużeniu DF. Stąd wycinek EDI > EDF 
oraz wycinek EDH < EDA. Ponadto:

Wówczas:

Stąd:

co należało udowodnić.■

Zauważmy, że długość łuku zawsze jest większa od długości stowarzyszonej z nim cięciwy i dlatego stosunek tych dwóch długości jest większy niż 1. Jednakże, jeśli drugi koniec łuku zbliża się do pierwszego i tym samym długość łuku i cięciwy zmniejsza się, to ich różnica jest coraz mniejsza, a stosunek tych dwóch wielkości zbliża się coraz bardziej do 1. Stosunek ten będzie równy 1, gdy drugi koniec łuku pokryje się z pierwszym.

W związku z tym, jeżeli założymy, że dwa łuki są tak małe, że ich długości nie różnią się znacząco od długości cięciw z nimi stowarzyszonych, to stosunek długości tych łuków będzie bliski stosunkowi stowarzyszonych z nimi cięciw.

Przykłady:

1. Wyliczyliśmy wcześniej, iż łukom 3° i 1 1/2° odpowiadają cięciwy równe w przybliżeniu: 0,0523521r oraz 0,0261782r. Sprawdźmy, czy teza powyższego twierdzenia zachodzi w tym przypadku. Istotnie: 

czyli:

2. Cięciwa stowarzyszona z łukiem 3/4° jest równa 0,0130894r. Sprawdźmy, czy powyższe twierdzenie jest prawdziwe dla łuków 1 1/2° oraz 3/4°:

Należy tutaj podkreślić, że Mikołaj Kopernik w swoim dziele De Revolutionibus wyliczył, iż z łukiem 1 1/2° stowarzyszona jest cięciwa długości 0,02618r, a z łukiem 3/4° cięciwa 0,01309r (zapis tych wyników został dostosowany do notacji przyjętej w niniejszej pracy). Jeżeli przyjąć wyliczenia Kopernika, to:

co oznaczałoby, że powyższe twierdzenie nie jest prawdziwe. Należy jednak zwrócić uwagę, że taka sytuacja jest skutkiem jedynie niedokładności obliczeń i dokonania zbyt dużego zaokrąglenia wyniku (sam Kopernik powyższą sytuację wyjaśnił niedokładnościami w obliczeniach, jednakże nie pokusił się o dokonanie bardziej dokładnych rachunków). Wyznaczenie długości cięciw stowarzyszonych z łukami 1 1/2° oraz 3/4° z większą dokładnością spowodowało, że teza powyższego twierdzenia dla tych łuków i odpowiadających im cięciw stała się prawdziwa.

Tabele - cięciwa koła

Rozdział XII Kopernik zakończył uporządkowaniem wszystkich łuków okręgu o promieniu 100 000 i o miarach od 0° do 90° w odstępach 10'. Umieścił je w tabeli, a następnie dla każdego z tych łuków obliczył połowę długości cięciwy stowarzyszonej z podwojonym tymże łukiem i wynik zapisał po prawej stronie miary łuku. Na przykład: dla łuku 90° długość połowy cięciwy stowarzyszonej z łukiem o mierze 180° (czyli 2 · 90°) wynosi 100000, a dla łuku 45° długość połowy cięciwy stowarzyszonej z łukiem o mierze 90° to 70711 (dzisiaj wiemy, że są to wartości przybliżone).

Jedną ze stron tejże tabeli umieszczona przez Kopernika w rękopisie jego dzieła De Revolutionibus, przedstawiono na ryc. 69.

Uwaga: 
Tabelę długości cięciw w kole o promieniu 100 000 ułożoną przez Kopernika można uogólnić poprzez rozważenie koła o dowolnym promieniu r. Wówczas połowa długości cięciwy stowarzyszonej z podwojonym łukiem (miara łuku dana w lewej kolumnie tabeli) będzie wynosiła w przybliżeniu:

(podana długość cięciwy w odpowiednim wierszu lewej kolumny tabeli), gdzie r jest promieniem rozważanego koła.
Rozważania przeprowadzone w XII rozdziale dzieła De Revolutionibus, a w szczególności tabele cięciw w kole, stanowiły bazę do rozwiązywania trójkątów płaskich. Temu zagadnieniu astronom poświęcił rozdział XIII Księgi I.

Bibliografia:

1. Tujakowski A., Mikołaja Kopernika „De Revolutionibus”, Historia wydań, Toruń 1973, s. 14.
2. Mikołaj Kopernik: O obrotach, [w:] Dobrzycki J. (red.), Mikołaj Kopernik: Dzieła wszystkie II, Polska Akademia Nauk, Państwowe Wydawnictwo Naukowe, Warszawa 1976.
3. Ibidem, s. 26.
4. Rheticus J., Baranowski J., Nicolai Copernici Thorunensis De Revolutionibus Orbium Coelestium Libri Sex, Mikołaja Kopernika Toruńczyka o Obrotach Ciał Niebieskich Ksiąg Sześć, Warszawa 1854, s. 546.
5. Ibidem, s. 547.
6. Mikołaj Kopernik: O obrotach, op. cit., s. 26–38.
7. Koppe K., Anfangsgründe der reinen Mathematik für der Schul- und 
8. Selbst-Unterricht, cz. II: Planimetrie (wyd. 4), Essen 1852, s. 131.
9. Mikołaj Kopernik: O obrotach, Op. cit., s. 29.
10. Rękopis dzieła Mikołaja Kopernika – O Obrotach – Facsimile, [w:] Czartoryski P. (red.), Mikołaj Kopernik: Dzieła wszystkie I, Warszawa – Kraków 1972, k. 18.