Na łamach marcowego i kwietniowego wydania „Matematyki” poruszamy temat nauczania trygonometrii przy wykorzystaniu metod stosowanych w XIX i XX wieku. Ponadto, w niniejszym numerze zamieszczamy przykładowe testy i sprawdziany z matematyki i rozpoczynamy nowy cykl artykułów Janusza Karkuta dotyczących nauczania matematyki z GeoGebrą. Seria krótkich tekstów świetnie pokazuje, w jakich celach nauczyciel może wykorzystać GeoGebrę na lekcjach matematyki.

Trygonometria nauczana metodą z XIX i XX wieku

„W XIX wieku w nauczaniu szkolnym matematyki funkcje trygonometryczne były wykorzystywane przede wszystkim do rozwiązywania trójkątów płaskich – znajdowania długości wszystkich boków i miar wszystkich kątów trójkąta w oparciu o pewne dane wyjściowe. W pierwszej części niniejszego artykułu zostały omówione zagadnienia z trygonometrii płaskiej umieszczone w podręczniku «Die Elementar Mathematik» [Matematyka elementarna] Ludwiga Kambly’ego. Tego podręcznika używano np. w gimnazjach w Toruniu i Bydgoszczy. W tej części artykułu zostanie rozwiązane przykładowe zadanie z podręcznika Kambly’ego. Będzie to zadanie typu: «rozwiąż trójkąt płaski». Rozwiązanie zostanie przeprowadzone na dwa sposoby: metodą z XIX oraz metodą z XX wieku” – pisze Karolina Karpińska w artykule zatytułowanym „Trygonometria płaska w gimnazjalnym nauczaniu matematyki w XIX wieku”. Niniejszy tekst zakończony jest komentarzem dotyczącym możliwości rozwiązywania zadań tego typu we współczesnej praktyce edukacyjnej.

Potęgi – zestaw zadań dla uczniów szkoły podstawowej

W bieżącym wydaniu czasopisma znajdą Państwo opracowanie autorstwa Agnieszki Zielińskiej zatytułowane „Potęgi”. Niniejszy zestaw zadań służy kształtowaniu umiejętności obliczania potęg liczb wymiernych o wykładnikach naturalnych, zapisywania w postaci jednej potęgi iloczynu i ilorazu potęg o takich samych podstawach, iloczynu i ilorazu potęg o takich samych wykładnikach, porównywania potęg o różnych wykładnikach naturalnych i takich samych podstawach oraz zamiany potęg o wykładnikach całkowitych ujemnych na odpowiednie potęgi o wykładnikach naturalnych.

Zadania na dowodzenie – trójkąt prostokątny

W rubryce „Koło matematyczne” publikujemy opracowanie Zygmunta Krawczyka zatytułowane „Trójkąt prostokątny – zadania na dowodzenie (cz. 9)”. W dziewiątej serii zadań poświęconych geometrii trójkąta prostokątnego autor prezentuje zadania na dowodzenie. „Część dowodów polega na sprawdzeniu ciekawych i zaskakujących zależności pomiędzy elementami trójkąta prostokątnego. Zwykle dowody można przeprowadzać różnymi sposobami, dlatego też nie podaję rozwiązań, aby nie sugerować metody dowodzenia. Dzięki temu można samodzielnie poszukiwać różnych metod dowodzenia, co jest bardzo kształcące” – dodaje Zygmunt Krawczyk.

Testy i sprawdziany z matematyki dla uczniów na wszystkich poziomach nauczania

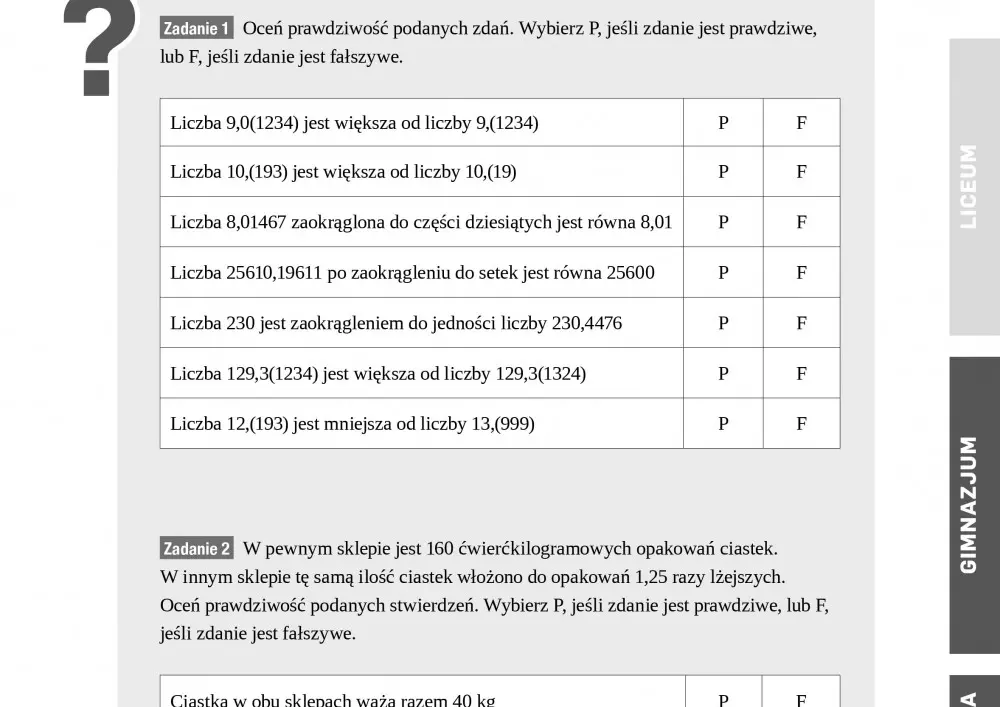
W bieżącym numerze czasopisma nie zabrakło przykładowych testów i sprawdzianów z matematyki oraz pomocy dydaktycznych ułatwiających codzienną pracę nauczyciela. Agnieszka Zielińska przekazuje Państwu dwa zestawy zadań adresowane do uczniów szkół podstawowych i gimnazjów, zaś Michał Kremzer przedstawia opracowanie dedykowane licealistom. Oprócz testów i sprawdzianów z matematyki, publikujemy również zadania sprawdzają następujące umiejętności: analizy i interpretacji problemu, rozumowania i argumentacji, syntezy faktów i myślenia pamięciowego oraz umiejętności heurystyczne.

Matematyka z GeoGebrą

Zachęcamy Państwa do lektury dwóch tekstów, które publikujemy w dziale „Nowe technologie w matematyce” – „Matematyka z GeoGebrą − cz. 1. Miara” i „Matematyka z GeoGebrą − cz. 2. Płaszczyzna Kartezjańska“. Pierwsza część nowej serii artykułów traktuje o odcinkach i ich długościach, podziale na (nie)równe części oraz zastosowaniach w niektórych zadaniach. Drugi tekst autorstwa Janusza Karkuta poświęcony jest elementom geometrii analitycznej.

Szeroki wachlarz zastosowań programu GeoGebra

W tej samej rubryce zamieszczamy jeszcze jeden artykuł poświęcony licznym zastosowaniom oprogramowania GeoGebra w nauczaniu matematyki. „Zadania problemowe to zadania nietypowe, a w związku z tym – niezwykle ciekawe. Rozwiązywanie ich uczy niestandardowego myślenia, rozwija pomysłowość i kreatywność. Świetnie sprawdzają się w połączeniu z GeoGebrą, z którą tworzą bardzo dobry zestaw na lekcję, zajęcia dodatkowe, do samodzielnej pracy uczniów, czy na zadanie domowe” – zapewnia Magdalena Żonierczyk w tekście zatytułowanym „Jedno zadanie, wiele możliwości”.