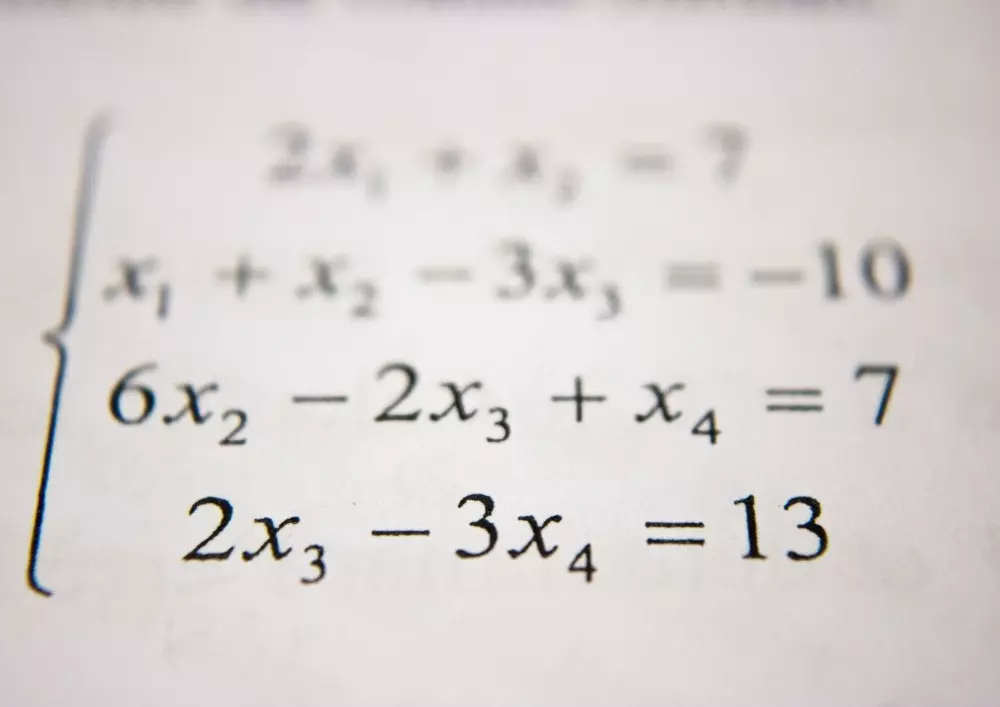W bieżącym wydaniu czasopisma kontynuujemy temat zastosowań wielokątów foremnych w sztuce i architekturze, publikujemy kolejny artykuł z cyklu dotyczącego nauczania matematyki z GeoGebrą i proponujemy nowatorski sposób wykonania papierowych modeli brył archimedesowych.

Ponadto, we wrześniu i październiku zamieszczamy przykładowe testy i sprawdziany z matematyki oraz zastanawiamy się, jakie miejsce w procesie dydaktycznym zajmują obecnie konstrukcje geometryczne.

Wielokąty foremne w sztuce islamu

Bieżący numer czasopisma otwiera druga część artykułu Mirosława Majewskiego pt. „Wielokąty foremne i gereh”. W niniejszym tekście autor przedstawia trzy typy geometrii wzorów wypełniających teselacje z wielokątami foremnymi – dwunastokątem, sześciokątem, kwadratem i trójkątem – oraz kilka wariantów tych wypełnień.

Liczby zespolone w edukacji matematycznej

„Już na początku naszej ery Heron z Aleksandrii, bawiąc się figurami i bryłami geometrycznymi, tworzył figury, które nie miały prawa istnieć w naszej rzeczywistości, ponieważ miały ujemną wysokość. Niestety, nie przywiązywał do tego zbyt dużej uwagi i odkrycie liczb zespolonych odsunęło się w czasie. Kolejnym Grekiem, który miał szansę zapisać się w historii matematyki złotymi głoskami jako odkrywca liczb zespolonych, był Diofantos. Diofantos zasłynął z tak zwanych równań diofantycznych (równania, których pierwiastków szukamy w zbiorze liczb całkowitych). Zajmując się trójkątami prostokątnymi, otarł się o liczby zespolone“ – pisze Maciej Nowakowski w arcyciekawym artykule zatytułowanym „Magiczne liczby zespolone”, który publikujemy w dziale „Koło matematyczne”. Zamieszczając niniejszy tekst staramy się Państwa przekonać, że liczby zespolone wnoszą bardzo dużo do naszego rozumienia rzeczywistości.

Bryły archimedesowe i ich ażurowe modele

W poprzednim numerze czasopisma „Matematyka” zajmowaliśmy się bryłami platońskimi. W bieżącym wydaniu publikujemy artykuł Tadeusza E. Dorozińskiego zatytułowany „Bryły archimedesowe nieco inaczej”. Czytając niniejszy tekst poznają Państwo ciekawą metodę wykonania nietypowych modeli brył archimedesowych.

Testy i sprawdziany z matematyki dla uczniów na wszystkich poziomach nauczania     

W bieżącym numerze czasopisma nie zabrakło przykładowych testów i sprawdzianów z matematyki oraz pomocy dydaktycznych ułatwiających codzienną pracę nauczyciela. We wrześniu i październiku Michał Kremzer przekazuje Państwu zestawy zadań adresowane do uczniów szkół podstawowych, gimnazjów i szkół średnich. Oprócz testów i sprawdzianów z matematyki, przedstawiamy również koncepcję sprawdzenia poprawności stosowania metodyki rozwiązywania zadań tekstowych. W niniejszym wydaniu „Matematyki” omawiamy szczegółowo jedno zadanie, na podstawie którego zaprezentowane zostaną pewne hipotezy i wskazania do kierunku dalszych badań.

Matematyka z GeoGebrą

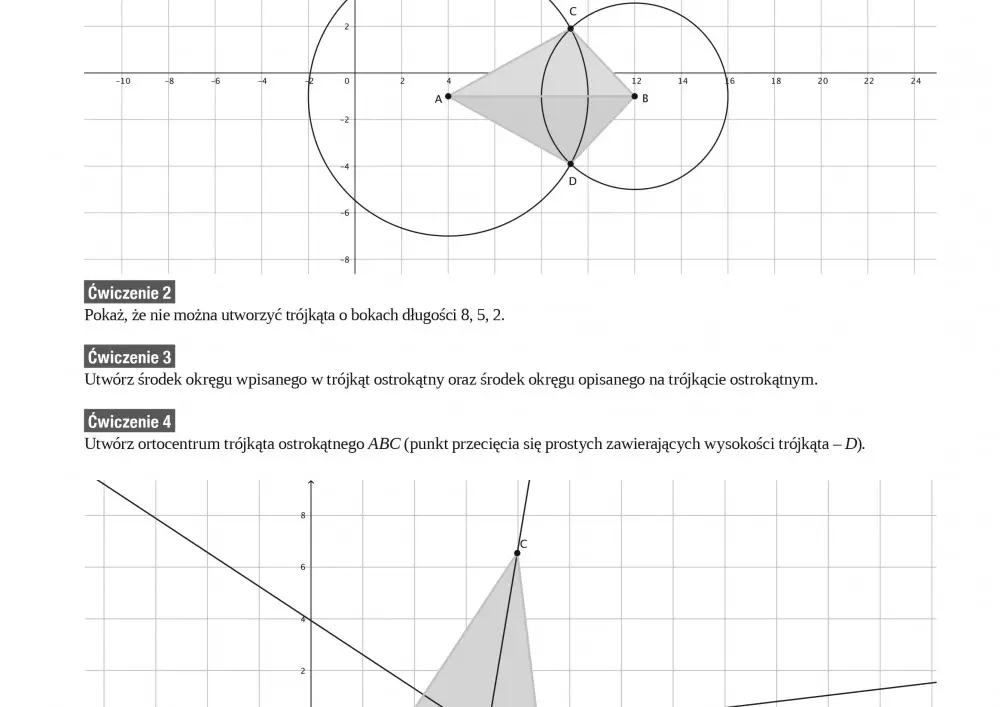
W rubryce „Nowe technologie w matematyce” znajdą Państwo tekst Janusza Karkuta zatytułowany „Matematyka z GeoGebrą. Punkty szczególne trójkąta”. Seria krótkich artykułów i dołączonych do nich ćwiczeń zainspiruje Państwa do nauczania matematyki z GeoGebrą – bezpłatnym oprogramowaniem edukacyjnym wspierającym uczniów i nauczycieli na wszystkich poziomach edukacji.

Konstrukcje geometryczne w nauczaniu matematyki

Pozostając wciąż w temacie nauczania matematyki z GeoGebrą – zachęcamy Państwa do lektury tekstu Magdaleny Żołnierczyk pt. „Konstrukcje geometryczne a GeoGebra”. Autorka przekonuje w nim, że „możemy wprowadzać na lekcjach praktycznie wszystkie omawiane podstawowe konstrukcje geometryczne, takie jak: proste prostopadła i równoległa przechodzące przez dany punkt, symetralna odcinka, dwusieczna kąta, styczna do okręgu czy okręgi wpisane i opisane. Jednak nie tylko na te konstrukcje powinniśmy znaleźć czas na naszych lekcjach. Mimo starań bardzo często te wyżej wymienione pojawiają się na lekcji jako gotowe schematy do nauczenia się przez ucznia. Często nie mamy czasu, albo nawet nie pomyślimy o tym, żeby pozwolić uczniom wpaść na pomysł, jak wykonać dany rysunek, mając tylko czystą kartkę, linijkę i cyrkiel. Co stoi na przeszkodzie, aby potraktować takie zagadnienia jak problem do rozwiązania? Uczniowie, którzy w szkole podstawowej nie zetkną się z konstrukcjami, z pewnością w szkole średniej chętnie popatrzą na takie zadania jak na problem, wręcz zagadkę. To, w jaki sposób możemy podejść do pewnych zagadnień, w dużej mierze zależy od zespołu klasowego, z jakim pracujemy, i od naszego wyczucia, na ile możemy sobie pozwolić”.