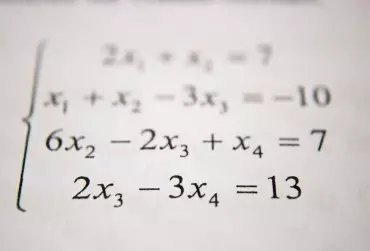Kategoria: Artykuły
Trygonometria jako nauka nie ulega zmianom, jednakże treści nauczania podyktowane oczekiwaniami programów uniwersyteckich i rynku pracy z pewnością różnią się pomiędzy krajami. W poniższym artykule chciałbym przedstawić zarys programu nauczania trygonometrii w szkołach średnich w USA.
Edukacja matematyki w szkole średniej kończy się na zbiorze liczb rzeczywistych. Prawdziwa przygoda zaczyna się w momencie, kiedy odkrywamy, że można pierwiastkować liczby ujemne. Mówimy wtedy o liczbach zespolonych i w tym artykule chciałbym je przedstawić.
Operatywne stosowanie narzędzi matematycznych do opisu sytuacji przedstawionej w rozpatrywanym problemie jest kluczową umiejętnością pozwalającą na prawidłowy rozwój matematyczny indywidualnego ucznia. Prawidłowa analiza zadania, zrozumienie problemu, zastanowienie się nad sposobem rozwiązania, wykonanie zaplanowanych czynności i w końcu spojrzenie na zadanie w sposób całościowy, stanowią fundament rozumowania, które prowadzi do abstrakcyjnego pojmowania rozważanych treści. Polyowska metoda rozwiązywania zadań tekstowych, modyfikowana ze względu na cyfryzację rzeczywistości, jest w dalszym ciągu podstawą pracy nauczyciela z uczniem.
W poprzedniej części tego szkicu pokazaliśmy, w jaki sposób, wypełniając wielokąty foremne – trójkąt, kwadrat, sześciokąt i dwunastokąt – różnego rodzaju wzorami, możemy skonstruować gereh. Omówiliśmy dwie grupy takich wzorów. Nazwaliśmy je umownie geometriami wzoru typu A i B. Wypełnienia w typie A były zależne od linii łączących środki boków trójkąta. Natomiast typ B otrzymaliśmy, łącząc liniami prostymi środki sąsiednich boków kwadratu. W tej części szkicu kontynuujemy nasze eksploracje.
Te słowa przyświecały zarówno prelegentom, jak i uczestnikom II Kongresu Matematyki, który odbył się 7 kwietnia 2017 r. w Warszawie. W wydarzeniu tym − zorganizowanym przez wydawnictwo Forum Media Polska − wzięło udział około 400 osób i każda z nich wyniosła dla siebie coś innego − za sprawą naszych prelegentów okazało się bowiem, że matematyka może szybko stać się pasją i można ją przekazywać na tysiąc sposobów.
Sieci płaskie mają wiele wspólnego z parkietażami. W tym cyklu artykułów pokażemy drogę, która poprowadzi nas od sieci płaskich do parkietaży – nie zawsze tak znanych, albo też i nowych, a czasem zaskakujących. Pojawi się też aspekt trzeciego wymiaru.
Zaprojektowanie siatki tego wielościanu nie należy do najłatwiejszych. Składa się ona z 6 gwiazd ośmiokątnych (oktagramów), 12 ścian sześciokątnych, 48 czworokątnych oraz 48 trójkątów prostokątnych – ryc. 1. Oktagramiczne ściany mają krawędzie tej samej długości co krawędzie ścian kwadratowych.
Chociaż zagadnienia związane z wektorami zostały przypisane do poziomu rozszerzonego wymagań maturalnych, to wielu nauczycieli decyduje się wprowadzić podstawy tego tematu we wszystkich swoich klasach.
Nie są to bowiem treści nazbyt skomplikowane, a ich znajomość może ułatwić omawianie innych tematów (na przykład związanych z przekształceniami wykresów funkcji). Ponadto z pojęciem wektora uczniowie mogą mieć styczność na innych przedmiotach, dlatego warto pokazać im matematyczne podejście do tego tematu, jeśli tylko mamy taką możliwość.