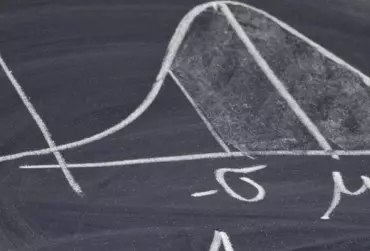W dwóch poprzednich odcinkach „Koła”1, 2 przedstawiłem Czytelnikom omówienie treści pewnego starego zadania z konkursu zadaniowego „Matematyki”. Zadanie to pochodzi od wybitnego polskiego matematyka, W. Sierpińskiego, a jego treść została opublikowana w „Matematyce” w 1977 r.3 – choć samo zadanie pochodziło jeszcze z 1958 r. – i brzmiała następująco: Liczba złożona. Znaleźć liczbę złożoną, która pozostanie złożoną przy każdej zmianie którejkolwiek z jej dwóch cyfr.
Kategoria: Artykuły
Iteracje są jednym z najbardziej podstawowych i najstarszych pojęć spotykanych w matematyce. W tym artykule będziemy koncentrować się na iteracjach obiektów geometrycznych – od tych najprostszych, czyli punktów i odcinków, do bardziej złożonych, takich jak kwadraty, wielokąty i inne figury. Pokażemy, jak takie iteracje można utworzyć w programie komputerowym do geometrii i jak można je wykorzystać na lekcji matematyki tak, aby uczeń mógł wynieść z lekcji coś więcej niż tylko ładny obrazek. Będziemy również zwracać uwagę na estetyczną stronę obiektów otrzymanych dzięki iteracjom, a więc będzie to jakiś krok w kierunku sztuki związanej z matematyką.
Kto z nauczycieli nie chciałby w trakcie prezentowania na lekcji stereometrii w szkole podstawowej lub liceum znanych wielościanów objętych programem nauczania i ich własności wzbogacić lekcji dynamicznym pokazem siatek tych wielościanów, wydrukować ich uczniom i rozdać do domu w celu ich sklejenia? To byłaby idealna lekcja stereometrii...
Matematycznych programów komputerowych możemy używać podczas naszych lekcji przy różnych okazjach. Będą one przydatne zarówno podczas wprowadzania nowych treści, jak i utrwalania zdobytej już wiedzy. Dlatego też polecam włączenie GeoGebry w proces przygotowań do różnego typu konkursów i egzaminów zewnętrznych.
Za oknem zima, słupek rtęci (lub innej substancji) oscyluje w okolicy zera. Hm… mówię jedną liczbę i wszyscy już wiedzą, że nie jest za ciepło. Innym razem wchodzę na wagę i kiedy wyświetla się… pewna liczba, to stwierdzam, że do lekkich osób nie należę. Czy wszystko da się tak ładnie opisać jedną liczbą? Czego tak naprawdę dowiaduję się, odczytując liczbę na podziałce termometru lub skali wagi? Czy ona mi wystarczy, aby dowiedzieć się precyzyjnie, czego potrzebuję?
Artykuł jest kontynuacją wprowadzenia pojęcia granicy jako narzędzia do analizowania funkcji wielomianowych, która była zapoczątkowana w poprzednim numerze „Matematyki”. I tak jak poprzednio skupiliśmy się na szczegółach wprowadzenia granicy funkcji do uczniowskiego słownika pojęć matematycznych na podstawie funkcji liniowych, tak ten artykuł poświęcony jest wykorzystaniu granic do analizowania funkcji kwadratowych.
Na co dzień mówimy o różnych zdarzeniach. W kontekście wielu zdarzeń dodajemy, że są mało prawdopodobne albo bardzo prawdopodobne, o dwu zdarzeniach mówimy, że jedno jest mniej prawdopodobne niż drugie, a inne dwa są jednakowo prawdopodobne. Wśród zdarzeń są prawie pewne i są prawie niemożliwe.
Treścią tego cyklu będą szerokie rozmyślania na temat związków matematyki z muzyką. Czytelnikowi nie zostanie przedstawiona żadna teoria, nie zostanie obroniona żadna hipoteza – poza tą, że matematyka i muzyka są ze sobą pewien sposób powiązane.
Gdy kończyłem poprzedni odcinek „Koła”, pisząc, że wkrótce wrócę do poruszanego tam tematu zadania Sierpińskiego o liczbach złożonych, nie przypuszczałem, że nastąpi to aż tak szybko. Z drugiej strony, odkładanie kontynuacji omówienia dowolnego zadania na zbyt odległą przyszłość w stosunku do momentu poprzedniego takiego omówienia jest niewątpliwie niekorzystne tak dla autora, jak i dla Czytelników tych omówień – traci się bowiem ciągłość. Dlatego w obecnym odcinku będziemy kontynuować zajmowanie się zadaniem Sierpińskiego, zwłaszcza że jego treść istotnie wymaga jeszcze dalszego przedyskutowania.
W poprzednich częściach tego szkicu pokazaliśmy, w jaki sposób, wypełniając wielokąty foremne – trójkąt, kwadrat, sześciokąt i dwunastokąt – różnego rodzaju wzorami możemy skonstruować gereh. Omówiliśmy trzy grupy takich wzorów. Nazwaliśmy je umownie geometriami wzoru typu A, B i C. Wypełnienia w typie A były zależne od linii łączących środki boków trójkąta równobocznego. Typ B otrzymaliśmy, łącząc liniami prostymi środki sąsiednich boków kwadratu. Wreszcie typ C otrzymaliśmy, łącząc środki sąsiednich boków sześciokąta foremnego. W tej części szkicu kontynuujemy nasze eksploracje.
Kolejny osiemnasty wielościan jednorodny znany w świecie matematycznym pod angielską nazwą Great Dodecisosahedron jest niezwykle prosty do utworzenia zarówno w znanym programie komputerowym SketchUp, jak i jako model kartonowy.