Proces nauczania jest kompleksowy, wielowarstwowy i na tyle skomplikowany, że wciąż prowadzi się dyskusje na jego temat. Czy to nauczanie problemowe, czy metoda heurystyczna – nie ma jednej recepty, która zapewniłaby pełny sukces. Wprowadzona przed 20 laty reforma bolońska szkolnictwa wyższego nie spełnia pokładanych w niej nadziei i jest coraz częściej krytykowana. To pokazuje, jak trudna jest to kwestia.
Kategoria: Artykuły
Mikołaj Kopernik (1473–1543) znany jest na całym świecie jako astronom, który „wstrzymał Słońce, a ruszył Ziemię” – zastąpił geocentryczny model świata Ptolemeusza modelem heliocentrycznym. Ale Kopernik to też matematyk...
Ogromna wszechstronność zastosowań GeoGebry to fakt, który dla jej licznych użytkowników jest oczywisty i niepodważalny. Jednak trzeba przyznać, że stosunkowo rzadko mówi się o wykorzystaniu arkusza kalkulacyjnego, który jest dołączony do programu. Dlatego też stwierdziłam, że warto poświęcić mu nieco więcej uwagi.
Spójrzmy na cechy podzielności z „niestandardowej” perspektywy. Przedstawiona propozycja może służyć m.in. nauczycielom i to w dwojaki sposób: może być konspektem lekcji w szkole ponadpodstawowej lub może być przedstawiona uczniom szkoły podstawowej na zajęciach dodatkowych.
Pojęcie granicy funkcji jest trudne do zrozumienia dla uczniów, gdyż istnieją różnorodne techniki liczenia granic w zależności od typu funkcji i typu granicy, którą student ma policzyć. Na przykład technika znalezienia granic jednostronnych dla funkcji logarytmicznych różni się od techniki znalezienia granic w nieskończoności dla tych samych funkcji. Ponieważ celem nauczania jest, by uczeń nie tylko poznał te techniki, ale też potrafił zrozumieć ich różnice, pamiętał je i właściwie je aplikował, różnorodność ta narzuca bardzo wnikliwą analizę metod wprowadzania tych zagadnień do praktyki szkolnej.
Matematycy uchodzą na ogół za ludzi skrajnie wręcz racjonalnych. Nic dziwnego, skoro od stuleci nasza dziedzina uprawiana jest w ramach rygorystycznie ścisłej dyscypliny intelektualnej. Ów rygor intelektualny, którego podwaliny sformułowane zostały jeszcze w IV w. p.n.e. przez Euklidesa1 w jego Elementach, wyrażany bywał później wielokrotnie przez kolejne wieki zarówno w podręcznikach matematyki, jak i w aforyzmach jej poświęconych.
Niniejszy tekst ma dwa cele. Pierwszym z nich jest pokazanie, w jaki sposób narzędzia definiowane przez użytkownika w programach komputerowych mogą posłużyć nam w nauczaniu elementów geometrii w szkole lub NIĄ. Drugim celem tego tekstu jest opisanie pewnej grupy wzorów geometrycznych określanych jako plecionki. Oba te cele świetnie integrują się w postaci gier lub układanek o charakterze matematycznym na dowolnym poziomie szkolnym. Wystarczy tylko zadbać o odpowiedni stopień trudności.
Niniejszy artykuł zostanie poświęcony omówieniu zmian, jakie zaszły w nauczaniu matematyki w szkołach średnich funkcjonujących na ziemiach polskich po odzyskaniu przez Polskę niepodległości w 1918 roku.
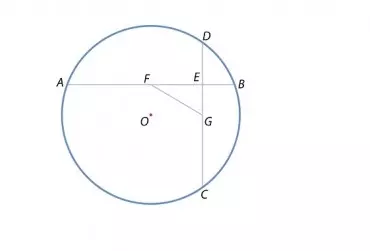
Jakie miejsce zajmują obecnie konstrukcje geometryczne w nauczaniu matematyki? Myślę, że trudno udzielić na to pytanie jednoznacznej odpowiedzi. Na pewno dużo zależy od indywidualnego podejścia nauczyciela i nacisku kładzionego przez niego na ten element edukacji matematycznej, jakim jest umiejętność wykonywania konstrukcji.