Gimnazja na przełomie XIX i XX wieku były szkołami przygotowującymi młodzież do studiów uniwersyteckich. W tym czasie cykl kształcenia w gimnazjach obejmował zazwyczaj dziewięć klas, były to (od najniższej do najwyższej): Sexta, Quinta, Quarta, Tertia Niższa, Tertia Wyższa, Secunda Niższa, Secunda Wyższa, Prima Niższa, Prima Wyższa. Nazwy klas wywodziły się z języka łacińskiego.
Kategoria: Artykuły
Gdy w 1957 roku Hugo Steinhaus opublikował w ramach „Konkursu zadaniowego” w „Matematyce”1 po raz pierwszy poniższe zadanie o wieżach na szachownicy, nie podejrzewał zapewne, że zadanie to – a właściwie jego rozwiązanie – będzie miało aż tak burzliwą historię.
Aktywne nauczanie matematyki stanowi jeden z głównych przedmiotów badań współczesnej dydaktyki matematyki. We współczesnej dydaktyce matematyki coraz większy nacisk kładzie się na aktywność twórczą, czynny i świadomy udział uczącego się w odkrywaniu pojęć, wzorów, twierdzeń, dowodów, w schematyzowaniu i matematyzowaniu sytuacji oraz rozwiązywaniu zróżnicowanych problemów obejmujących całość nauczanego materiału.
W ostatnich latach coraz częściej podkreśla się, że małe dzieci są matematycznie dużo bardziej kompetentne niż potocznie sądzimy. Nie tylko w spontaniczny sposób nabywają matematycznych sprawności, ale również są w stanie uczyć się trudniejszej (szerszej) matematyki niż ta, która tradycyjnie znajduje się w programach nauczania.
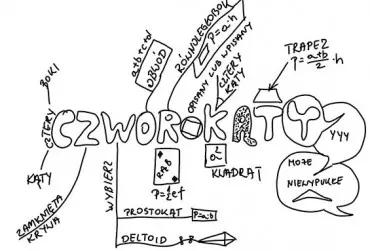
W poprzednim szkicu wspomnieliśmy o pracach Keplera nad teselacjami i jego eksperymentach z teselacjami z wielokątów foremnych. W tym szkicu wrócimy do Keplera, wprowadzimy pewne niezbędne określenia, a następnie zobaczymy, jaki związek mają próby Keplera z badaniami teselacji w matematyce współczesnej.
Nieraz możemy spotkać się z sytuacją, gdy uczeń podczas lekcji buja w obłokach. Jest to sygnał dla nauczyciela, że to, co się dzieje w klasie, dla mózgu tego konkretnego ucznia jest mało atrakcyjne. Co możemy zaproponować uczniom, aby lekcje stały się ciekawsze (przynajmniej z punktu widzenia mózgu)? Jakie techniki zastosować na matematyce?
Matematyka – królowa nauk...., niestety też królowa uczniowskich koszmarów. Ostre słowa, ale jakże prawdziwe i potrzebne w edukacji XXI wieku. Co by było, gdyby zamiast zapowiedzianej kartkówki z określonej partii materiału, na ucznia czekała świetna zabawa w zgranym zespole z matematyką w tle?
Sześcian jest jedną z najbardziej rozpowszechnionych brył w otaczającej nas rzeczywistości. Jego regularne kształty i własności geometryczne powodują, że architekci, konstruktorzy, artyści chętnie sięgają po ten wielościan. Pojęcie sześcianu pojawia się w szkole stosunkowo wcześnie, jednak bryła ta i pojęcia podstawowe, które są z nią związane, często są traktowane nieco „po macoszemu”, nie doceniając znaczenia, jakie ma ten wielościan przy zrozumieniu własności bardziej złożonych brył. W jaki sposób wykorzystać modele sześcianów ze świata realnego do omówienia siatek sześcianu?
Programy nauczania matematyki obejmują te umiejętności, które są wspólne dla wszystkich. Wydaje się, że tych wspólnych, uniwersalnych umiejętności matematycznych jest w szkole coraz mniej. Obecne programy nauczania dla wszystkich dają mniej więcej połowę tego czasu, który był przeznaczany na matematykę kiedyś. Jest więc potrzeba uzupełniania tego dla chętnych. Może to być zdobywanie sprawności, które są pozaprogramowe. Jedną z takich sprawności może być „fotografowanie geometrii”.
Dobre przygotowanie naszych uczniów do egzaminów jest istotną częścią naszej pracy. I chociaż na co dzień dokładamy wiele starań, aby nasi podopieczni uzyskali wysokie wyniki, bywa tak, że efekty nie są zadowalające. Zaprezentuję ogólne tendencje, jakie od lat widoczne są przy analizie egzaminów zewnętrznych z matematyki, ze szczególnym uwzględnieniem testu pisanego po szkole podstawowej.
Technologie informacyjno-komunikacyjne mogą być wykorzystywane przez nauczyciela na wiele sposobów. Należy jedynie pamiętać, że nie mogą one być ozdobnikiem lekcji, lecz mają pomagać uczniowi uczyć się, zwiększać jego motywację do nauki i efektywność tej nauki oraz wspierać jego rozwój. Zatem z jakich narzędzi TIK korzystać na lekcjach matematyki, aby rozwijać u uczniów umiejętności przedmiotowe, kompetencje cyfrowe oraz umiejętności uczenia się?
Już Blaise Pascal twierdził, że matematyka jest dziedziną tak poważną, że nie wolno zmarnować żadnej okazji, by uczynić ją bardziej zabawną. Ojciec Leon z kolei uważa, że radość z życia jeszcze nikomu nie zaszkodziła. W Japonii natomiast znane jest przysłowie, według którego z uśmiechem na twarzy człowiek podwaja swoje możliwości. A czym jest uśmiech dla matematyka?